На некотором кондитерском заводе произошла очередная оптимизация линии по производству тортов, и теперь торты выпускаются сразу партиями по $$$n$$$ штук! На последнем этапе сборки тортов все $$$n$$$ тортов должны быть одновременно политы кремом.
Рассмотрим вид сбоку на конвейерную ленту, представим ее в виде числовой прямой. $$$i$$$-й торт занимает отрезок $$$[a_i - w, a_i + w]$$$ на этой прямой, любая пара отрезков не имеет общих точек. Над конвейером расположены $$$n$$$ дозаторов, при нажатии на общую кнопку из $$$i$$$-го дозатора выльется крем на отрезок конвейера $$$[b_i - h, b_i + h]$$$. Любая пара этих отрезков также не имеет общих точек.
 Торты и дозаторы, соответствующие первому примеру.
Торты и дозаторы, соответствующие первому примеру. Настройку этой части конвейера еще не проводили, поэтому ее нужно выполнить вам. Определите, можно ли подвинуть конвейер так, чтобы крем попал на каждый торт, и при этом не вытек за пределы тортов? Можете считать, что конвейер достаточно длинный, и торты с него никогда не падают. Также учтите, что кнопку можно нажать лишь один раз.
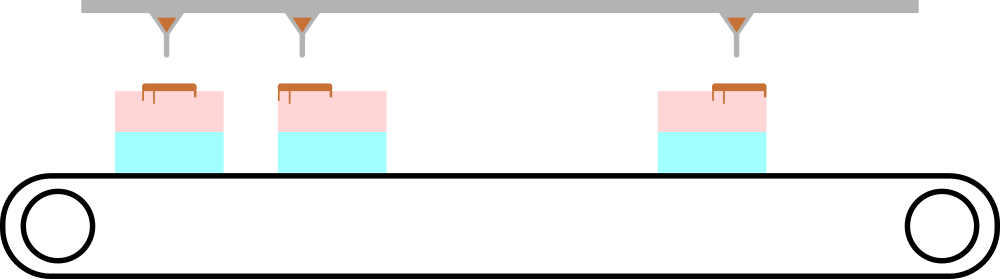 В первом примере можно подвинуть торты как показано на рисунке.
В первом примере можно подвинуть торты как показано на рисунке. Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 10^5$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит три целых числа $$$n$$$, $$$w$$$ и $$$h$$$ ($$$1 \le n \le 10^5$$$; $$$1 \le w, h \le 10^5$$$; $$$h \le w$$$) — количество тортов и дозаторов, а также полуширины тортов и участков, на которые выливается крем.
Вторая строка каждого набора содержит $$$n$$$ целых чисел $$$a_1$$$, $$$a_2$$$, ..., $$$a_n$$$ ($$$1 \le a_i \le 10^9$$$) — положения центров тортов. Гарантируется, что $$$a_i + w < a_{i + 1} - w$$$ для всех $$$i$$$.
Третья строка каждого набора содержит $$$n$$$ целых чисел $$$b_1$$$, $$$b_2$$$, ..., $$$b_n$$$ ($$$1 \le b_i \le 10^9$$$) — положения дозаторов. Гарантируется, что $$$b_i + h < b_{i + 1} - h$$$ для всех $$$i$$$.
Гарантируется, что сумма значений $$$n$$$ по всем наборам входных данных не превосходит $$$10^5$$$.
Для каждого набора входных данных выведите «YES», если можно подвинуть конвейер так, чтобы крем попал на каждый торт, и не вытек за пределы тортов, и «NO» иначе.
Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ.
43 10 565 95 16540 65 1455 2 11 6 11 16 214 9 14 19 243 3 213 22 295 16 254 4 127 36 127 13635 50 141 144
YES YES NO YES
Первый пример показан на рисунках в условии.
Во втором примере мы можем подвинуть торты например так, чтобы их центры находились в позициях $$$4, 9, 14, 19, 24$$$.
В третьем примере подвинуть торты необходимым образом не получится.
| Название |
|---|




