| Codeforces Round 847 (Div. 3) |
|---|
| Закончено |
Вам дан неориентированный связный граф, в некоторых вершинах которого находятся фишки и/или бонусы. Рассмотрим игру, в которой участвует один игрок — вы.
Вы можете передвигать фишки согласно следующим правилам:
- В начале игры вы можете совершить ровно один ход: подвинуть любую фишку на любую соседнюю вершину.
- Если перемещение фишки завершилось на бонусе, то разрешается совершить ещё один ход любой другой фишкой.
Можно использовать разные бонусы в любом порядке, один и тот же бонус может быть использован несколько раз. Бонусы в ходе игры не перемещаются.
В одной вершине может одновременно находиться несколько фишек, но изначально в каждой вершине находится не более одной фишки.
Вершина с номером $$$1$$$ является финишной, и ваша задача — определить, можно ли попасть в неё какой-либо фишкой, совершая ходы фишками по описанным выше правилам. Если какая-то фишка изначально находится в вершине $$$1$$$, то игра считается уже выигранной.
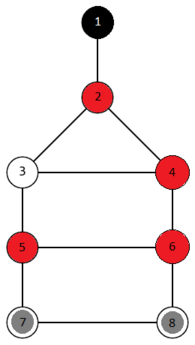 Финиш обозначен чёрным цветом, бонусы красным, фишки — серым.
Финиш обозначен чёрным цветом, бонусы красным, фишки — серым. - Перейти из $$$8$$$-й вершины в $$$6$$$-ю.
- Перейти из $$$7$$$-й вершины в $$$5$$$-ю.
- Перейти из $$$6$$$-й вершины в $$$4$$$-ю.
- Перейти из $$$5$$$-й вершины в $$$6$$$-ю.
- Перейти из $$$4$$$-й вершины в $$$2$$$-ю.
- Перейти из $$$6$$$-й вершины в $$$4$$$-ю.
- Перейти из $$$2$$$-й вершины в $$$1$$$-ю, которая является финишной.
Первая строка входных данных содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следуют описания наборов входных данных.
Первая строка описания каждого набора входных данных содержит два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n \le 2 \cdot 10^5$$$, $$$0 \le m \le 2 \cdot 10^5$$$) — число вершин и рёбер в графе, соответственно.
Вторая строка описания каждого набора входных данных содержит два целых числа $$$p$$$ и $$$b$$$ ($$$1 \le p \le n, 0 \le b \le n$$$) — число фишек и бонусов, соответственно.
Третья строка описания каждого набора входных данных содержит $$$p$$$ различных целых чисел от $$$1$$$ до $$$n$$$ — номера вершин, в которых находятся фишки.
Четвёртая строка описания каждого набора входных данных содержит $$$b$$$ различных целых чисел от $$$1$$$ до $$$n$$$ — номера вершин, в которых находятся бонусы. Обратите внимание, что значение $$$b$$$ может быть равно $$$0$$$. В этом случае эта строка является пустой.
В одной вершине могут одновременно находиться и фишка и бонус.
Следующие $$$m$$$ строк описания каждого набора входных данных содержат по два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$u_i \ne v_i$$$) — вершины, соединяемые $$$i$$$-м ребром. Между каждой парой вершин существует не более одного ребра. Заданный граф является связным, то есть из любой вершины можно попасть в любую, двигаясь по рёбрам.
Наборы входных данных разделены пустой строкой.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$. Аналогично, гарантируется, что сумма $$$m$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных в отдельной строке выведите YES, если можно дойти до финиша какой-нибудь фишкой, и NO в противном случае.
Вы можете выводить YES и NO в любом регистре (например, строки yEs, yes, Yes и YES будут распознаны как положительный ответ).
68 102 47 82 4 5 61 22 32 43 43 54 65 65 76 87 85 41 1531 22 33 44 52 11 021 24 31 223 41 22 32 45 43 25 3 42 41 22 33 44 51 01 111
YES NO YES YES YES YES
- Первый набор входных данных разобран в условии.
- Во втором наборе входных данных есть только одна фишка, она может походить только один раз, и не может дойти до финиша.
- В третьем наборе входных данных фишка может дойти до финиша за $$$1$$$ ход.
- В четвёртом наборе входных данных нужно просто походить от вершины $$$2$$$ к вершине $$$1$$$.
- В шестом наборе входных данных фишка изначально находится в вершине номер $$$1$$$, поэтому мы побеждаем сразу.
| Название |
|---|




