| Codeforces Round 849 (Div. 4) |
|---|
| Закончено |
Альперен стоит в точке $$$(0,0)$$$. Ему дана строка $$$s$$$ длины $$$n$$$ и он производит $$$n$$$ перемещений: $$$i$$$-е перемещение происходит так:
- если $$$s_i = \texttt{L}$$$, он перемещается на одну клетку влево;
- если $$$s_i = \texttt{R}$$$, он перемещается на одну клетку вправо;
- если $$$s_i = \texttt{U}$$$, он перемещается на одну клетку вверх;
- если $$$s_i = \texttt{D}$$$, он перемещается на одну клетку вниз.
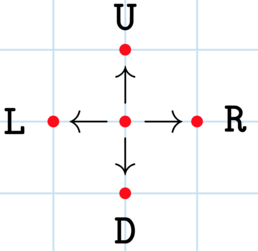 Если Альперен начинает в точке в центре, он может сделать четыре различных перемещения, как показано на рисунке.
Если Альперен начинает в точке в центре, он может сделать четыре различных перемещения, как показано на рисунке. 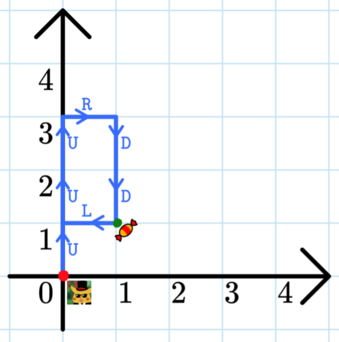 Alperen's path in the first test case.
Alperen's path in the first test case. Первая строка содержит целое число $$$t$$$ ($$$1 \leq t \leq 1000$$$) — количество наборов входных данных.
Первая строка каждого набора содержит целое число $$$n$$$ ($$$1 \leq n \leq 50$$$) — длину строки.
Вторая строка каждого набора содержит строку $$$s$$$ длины $$$n$$$ состоящую из символов $$$\texttt{L}$$$, $$$\texttt{R}$$$, $$$\texttt{D}$$$, и $$$\texttt{U}$$$, обозначающую перемещения Альперена.
Для каждого набора входных данных выведите «YES» (без кавычек), если Альперен доберется до конфеты, в противном случае, выведите «NO» (без кавычек).
Вы можете выводить ответ в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ).
77UUURDDL2UR8RRRUUDDD3LLL4DUUR5RUDLL11LLLLDDRUDRD
YES YES NO NO YES YES NO
В первом наборе входных данных Альперен следует по пути $$$$$$(0,0) \overset{\texttt{U}}{\to} (0,1) \overset{\texttt{U}}{\to} (0,2) \overset{\texttt{U}}{\to} (0,3) \overset{\texttt{R}}{\to} (1,3) \overset{\texttt{D}}{\to} (1,2) \overset{\texttt{D}}{\to} \color{green}{\mathbf{(1,1)}} \overset{\texttt{L}}{\to} (0,1).$$$$$$ Обратите внимание, что Альперену не обязательно находится в точке $$$(1,1)$$$ в конце своего пути, ему достаточно оказаться там хотя бы раз за весь путь.
Во втором наборе Альперен следует по пути $$$$$$(0,0) \overset{\texttt{U}}{\to} (0,1) \overset{\texttt{R}}{\to} \color{green}{\mathbf{(1,1)}}.$$$$$$
В третьем наборе Альперен следует по пути $$$$$$(0,0) \overset{\texttt{R}}{\to} (1,0) \overset{\texttt{R}}{\to} (2,0) \overset{\texttt{R}}{\to} (3,0) \overset{\texttt{U}}{\to} (3,1) \overset{\texttt{U}}{\to} (3,2) \overset{\texttt{D}}{\to} (3,1) \overset{\texttt{D}}{\to} (3,0) \overset{\texttt{D}}{\to} (3,-1).$$$$$$
В четвертом наборе Альперен следует по пути $$$$$$(0,0) \overset{\texttt{L}}{\to} (-1,0) \overset{\texttt{L}}{\to} (-2,0) \overset{\texttt{L}}{\to} (-3,0).$$$$$$
| Название |
|---|




