| Codeforces Round 869 (Div. 1) |
|---|
| Закончено |
Рассмотрим автомат с игрушками, в котором игрушки расположены в два ряда по $$$n$$$ ячеек каждый ($$$n$$$ — нечетное).
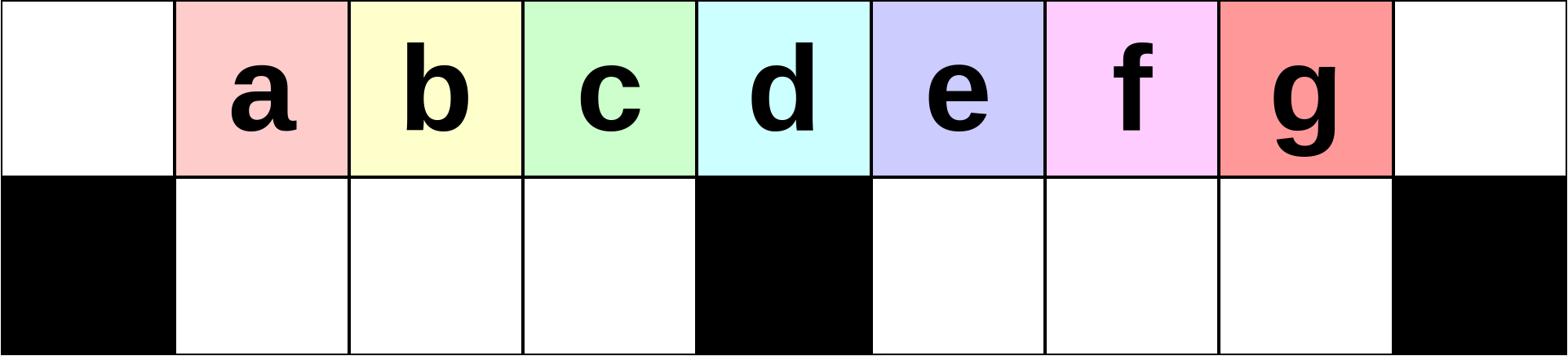 Начальное состояние для $$$n=9$$$.
Начальное состояние для $$$n=9$$$. Изначально в верхнем ряду в неугловых ячейках размещены $$$n-2$$$ игрушки. Нижний ряд изначально пуст, и его левая, правая и центральная ячейки заблокированы. Есть $$$4$$$ кнопки для управления автоматом: влево, вправо, вверх и вниз, обозначенные буквами L, R, U и D соответственно.
При нажатии на L, R, U или D все игрушки будут одновременно двигаться в соответствующем направлении и остановятся, только если они столкнутся с другой игрушкой, стеной или заблокированной ячейкой. Ваша цель — переместить $$$k$$$-ю игрушку в крайнюю левую ячейку верхнего ряда. Игрушки пронумерованы с $$$1$$$ по $$$n-2$$$ слева направо. Вам даны $$$n$$$ и $$$k$$$, найдите решение, которое использует не более $$$1\,000\,000$$$ нажатий кнопок.
Чтобы опробовать автомат, вы можете воспользоваться веб-страницей, позволяющей вам играть в описанную игру в режиме реального времени.
Первая и единственная строка содержит два целых числа $$$n$$$ и $$$k$$$ ($$$5 \le n \le 100\,000$$$, $$$n$$$ — нечетное, $$$1 \le k \le n-2$$$) — количество ячеек в ряду и номер игрушки, которую нужно переместить в крайнюю левую ячейку верхнего ряда.
Выведите описание нажатий кнопок в виде строки из не более чем $$$1\,000\,000$$$ символов. Строка должна содержать только символы L, R, U и D. $$$i$$$-й символ в строке соответствует $$$i$$$-й нажатой кнопке. После нажатия всех кнопок в указанной последовательности $$$k$$$-я игрушка должна быть в крайней левой ячейке верхнего ряда.
Если существует несколько решений, выведите любое из них. Количество нажатий кнопок не обязательно должно быть минимальным.
5 1
RDL
7 2
RDL
В первом примере будет $$$5-2 = 3$$$ игрушки. Первая игрушка должна оказаться в крайней левой ячейке верхнего ряда. Ходы RDL позволят достичь этого, см. картинку для лучшего понимания. Другим возможным решением было бы выполнить одно нажатие кнопки L.
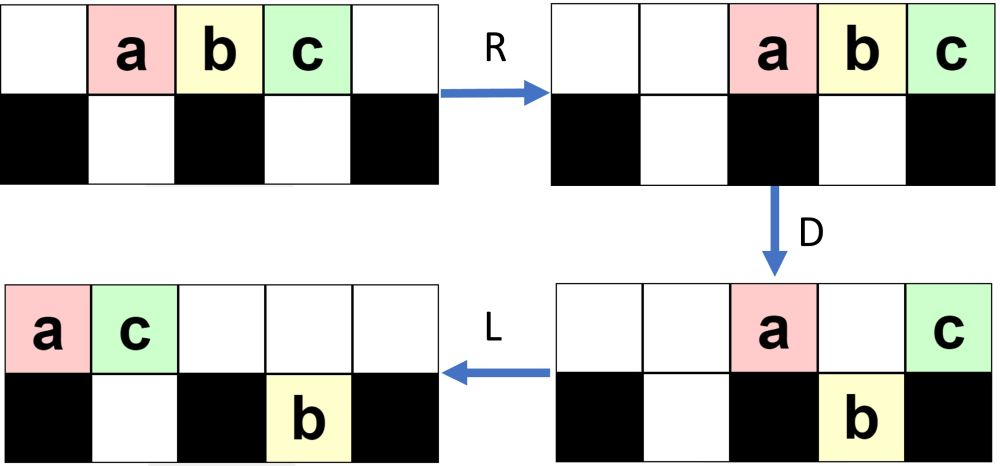 Визуализация ходов для первого примера.
Визуализация ходов для первого примера.
| Название |
|---|




