| Codeforces Round 896 (Div. 2) |
|---|
| Закончено |
Piggy живет на бесконечной плоскости с декартовой системой координат.
На плоскости есть $$$n$$$ городов, пронумерованных от $$$1$$$ до $$$n$$$, и первые $$$k$$$ городов являются крупными. Координаты $$$i$$$-го города равны $$$(x_i,y_i)$$$.
Piggy, как опытный путешественник, хочет совершить расслабляющую поездку после экзамена. В данный момент он находится в городе $$$a$$$, и хочет добраться до города $$$b$$$ на самолете. Между любыми двумя городами можно совершить перелёт, а также можно посещать несколько городов во время путешествия, но конечным пунктом должен быть город $$$b$$$.
Из-за активной торговли между крупными городами можно путешествовать на самолете между ними бесплатно. Формально, цена авиабилета $$$f(i,j)$$$ между двумя городами $$$i$$$ и $$$j$$$ определяется следующим образом:
$$$$$$ f(i,j)= \begin{cases} 0, & \text{если оба города }i \text{ и }j \text{ являются крупными городами} \\ |x_i-x_j|+|y_i-y_j|, & \text{в противном случае} \end{cases} $$$$$$
Piggy не хочет экономить время, но хочет сэкономить деньги. Поэтому вам нужно сказать ему минимальное значение суммарной стоимости всех авиабилетов, если он может совершить произвольное количество перелётов.
Первая строка входных данных содержит одно целое число $$$t$$$ ($$$1\le t\le 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит четыре целых числа $$$n$$$, $$$k$$$, $$$a$$$ и $$$b$$$ ($$$2\le n\le 2\cdot 10^5$$$, $$$0\le k\le n$$$, $$$1\le a,b\le n$$$, $$$a\ne b$$$) — количество городов, количество крупных городов и номера начального и конечного городов.
Затем следуют $$$n$$$ строк, $$$i$$$-я строка содержит два целых числа $$$x_i$$$ и $$$y_i$$$ ($$$-10^9\le x_i,y_i\le 10^9$$$) — координаты $$$i$$$-го города. Первые $$$k$$$ строк описывают крупные города. Гарантируется, что все координаты попарно различны.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$2\cdot 10^5$$$.
Для каждого набора входных данных выведите одно целое число — минимальное значение суммарной стоимости всех авиабилетов.
56 2 3 50 01 -2-2 1-1 32 -2-3 -32 0 1 2-1000000000 -10000000001000000000 10000000007 5 4 2154 147-154 -147123 45620 2343 20998 244353 1003 1 3 10 101 202 304 3 2 40 0-100 100-1 -1-1 0
4 4000000000 0 22 1
В первом наборе входных данных:
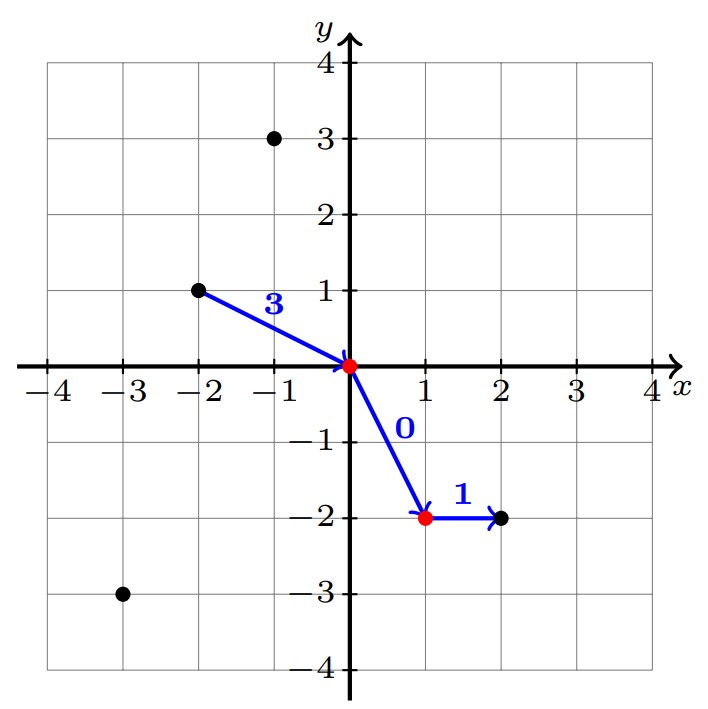 Крупные города отмечены красным.
Крупные города отмечены красным. Оптимальный способ выбора перелётов: $$$3\rightarrow 1 \rightarrow 2 \rightarrow 5$$$, что будет стоить $$$3+0+1=4$$$. Обратите внимание, что перелёт $$$1\rightarrow 2$$$ стоит $$$0$$$, потому что города $$$1$$$ и $$$2$$$ являются крупными городами.
Во втором наборе входных данных, так как всего $$$2$$$ города, единственный способ — совершить перелёт из города $$$1$$$ в город $$$2$$$.
В третьем наборе входных данных, так как города $$$2$$$ и $$$4$$$ являются крупными городами, Piggy может взять прямой рейс из города $$$2$$$ в город $$$4$$$, что будет стоить $$$0$$$.
В четвертом наборе входных данных, Piggy может совершить перелёты $$$3\rightarrow 2\rightarrow 1$$$, и стоимость будет $$$11+11=22$$$.
| Название |
|---|




