| Codeforces Round 900 (Div. 3) |
|---|
| Закончено |
После (наконец-то) прохождения отбора на IOI 2023, wxhtzdy был очень счастлив и решил сделать то, что делают многие люди: попытаться угадать задачи, которые будут на IOI. В процессе этого он случайно создал задачу, которая, по его мнению, была очень крутой.
Дано дерево (связный ациклический граф) с $$$n$$$ вершинами и $$$n-1$$$ ребром. Вершине $$$i$$$ ($$$1 \le i \le n$$$) соответствует значение $$$a_i$$$. Пусть $$$g(u, v)$$$ - это побитовое ИЛИ значений всех вершин на кратчайшем пути от $$$u$$$ до $$$v$$$. Например, если мы хотим вычислить $$$g(3, 4)$$$ на дереве из первого набора данных примера. На пути от $$$3$$$ до $$$4$$$ находятся вершины $$$3$$$, $$$1$$$, $$$4$$$. Тогда $$$g(3, 4) = a_3 \ | \ a_1 \ | \ a_4$$$ (здесь $$$|$$$ обозначает побитовое ИЛИ).
Также дано $$$q$$$ запросов, и каждый запрос выглядит следующим образом:
Вам даны $$$x$$$ и $$$y$$$. Рассмотрим все вершины $$$z$$$ такие, что $$$z$$$ находится на кратчайшем пути от $$$x$$$ до $$$y$$$ (включительно).
Определим красоту вершины $$$z$$$ как сумму количества ненулевых битов в $$$g(x, z)$$$ и количества ненулевых битов в $$$g(y, z)$$$. Вам нужно найти максимальную красоту среди всех вершин $$$z$$$ на кратчайшем пути от $$$x$$$ до $$$y$$$.
Так как его мозг очень устал после решения output only задачи на SIO (он должен был это сделать, чтобы пройти отбор на IOI), он хочет вашей помощи в этой задаче.
Первая строка ввода содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
Первая строка каждого набора содержит одно целое число $$$n$$$ ($$$1 \le n \le 2 \cdot 10^5$$$) — количество вершин.
Вторая строка каждого набора содержит $$$n$$$ положительных целых чисел $$$a_1, a_2, \dots, a_n$$$ ($$$1 \le a_v \le 10^9$$$) — значение каждой вершины, $$$i$$$-е число в этой строке соответствует вершине $$$i$$$.
Следующие $$$n - 1$$$ строк описывают дерево.
Каждая строка содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u, v \le n, u \ne v$$$) указывающие, что вершины $$$u$$$ и $$$v$$$ соединены ребром.
Следующая строка содержит одно целое число $$$q$$$ ($$$1 \le q \le 10^5$$$) — количество запросов.
Следующие $$$q$$$ строк содержат 2 целых числа $$$x, y$$$ ($$$1 \le x, y \le n$$$) — вершины $$$x$$$ и $$$y$$$ для каждого запроса.
Гарантируется, что сумма $$$n$$$ по всем наборам не превышает $$$2 \cdot 10^5$$$.
Гарантируется, что сумма $$$q$$$ по всем наборам не превышает $$$10^5$$$.
Для каждого набора входных данных выведите $$$q$$$ целых чисел, каждое из которых является ответом на соответствующий запрос.
341 2 3 41 31 21 431 11 31 437 6 33 12 141 11 21 32 31411 1
2 4 3 6 6 6 6 2
374 7 7 4 10 8 106 13 12 17 41 54 247 52 34 52 569 5 6 2 4 65 12 11 64 31 346 11 44 33 575 1 3 7 5 1 62 15 42 33 47 66 324 27 7
8 6 7 7 6 6 4 7 6 4
176 8 7 2 5 8 72 13 24 34 64 56 741 56 74 51 4
7 7 5 7
На изображении ниже показано дерево из первого набора входных данных второго примера.
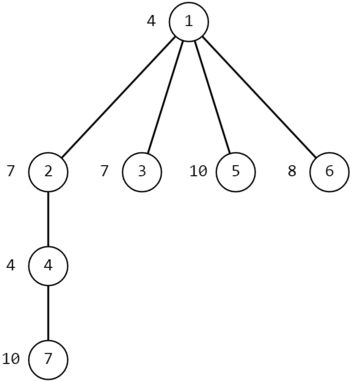 Дерево из первого набора входных данных второго примера.
Дерево из первого набора входных данных второго примера. В первом запросе $$$x=7$$$, $$$y=5$$$. Самый короткий путь от $$$7$$$ до $$$5$$$ это $$$7-4-2-1-5$$$.
Давайте вычислим красоту вершины $$$7$$$ на этом пути. У нас есть $$$g(7,7)=a_7=10=(1010)_2$$$ и $$$g(5,7)=a_5 \ | \ a_1 \ | \ a_2 \ | \ a_4 \ | \ a_7=10 \ | \ 4 \ | \ 7 \ | \ 4 \ | \ 10=15=(1111)_2$$$, поэтому ее красота равна $$$2 + 4 = 6$$$.
Теперь давайте вычислим красоту вершины $$$4$$$ на этом пути. У нас есть $$$g(7,4)=a_7 \ | \ a_4=10 \ | \ 4=14=(1110)_2$$$ и $$$g(5,4)=a_5 \ | \ a_1 \ | \ a_2 \ | \ a_4=10 \ | \ 4 \ | \ 7 \ | \ 4=15=(1111)_2$$$, поэтому ее красота равна $$$3 + 4 = 7$$$.
Теперь давайте вычислим красоту вершины $$$2$$$ на этом пути. У нас есть $$$g(7,2)=a_7 \ | \ a_4 \ | \ a_2=10 \ | \ 4 \ | \ 7=15=(1111)_2$$$ и $$$g(5,2)=a_5 \ | \ a_1 \ | \ a_2=10 \ | \ 4 \ | \ 7=15=(1111)_2$$$, поэтому ее красота равна $$$4 + 4 = 8$$$.
Теперь давайте вычислим красоту вершины $$$1$$$ на этом пути. У нас есть $$$g(7,1)=a_7 \ | \ a_4 \ | \ a_2 \ | \ a_1=10 \ | \ 4 \ | \ 7 \ | \ 4=15=(1111)_2$$$ и $$$g(5,1)=a_5 \ | \ a_1=10 \ | \ 4=14=(1110)_2$$$, поэтому ее красота равна $$$4 + 3 = 7$$$.
Наконец, давайте вычислим красоту вершины $$$5$$$ на этом пути. У нас есть $$$g(7,5)=a_7 \ | \ a_4 \ | \ a_2 \ | \ a_1 \ | \ a_5=10 \ | \ 4 \ | \ 7 \ | \ 4 \ | \ 10=15=(1111)_2$$$ и $$$g(5,5)=a_5=10=(1010)_2$$$, поэтому ее красота равна $$$4 + 2 = 6$$$.
Максимальная красота на этом пути у вершины $$$2$$$, и она равна $$$8$$$.
| Название |
|---|




