| Codeforces Round 928 (Div. 4) |
|---|
| Закончено |
У Владислава есть квадратное клетчатое поле размером $$$7 \times 7$$$, где каждая клетка окрашена в черный или белый цвет. За одну операцию можно выбрать любую клетку и изменить её цвет (черный $$$\leftrightarrow$$$ белый).
Найдите минимальное количество операций, необходимых для того, чтобы гарантировать, что нет черных клеток, у которых все четыре диагональных соседа также черные.
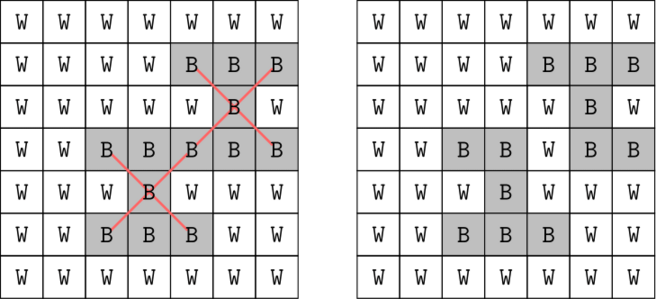
На левом изображении показано, что изначально есть две черные клетки, нарушающие условие. Переворачивая одну клетку, поле будет соответствовать требованию.
Первая строка ввода содержит одно целое число $$$t$$$ ($$$1 \leq t \leq 200$$$) — количество наборов входных данных. Затем следует описание наборов.
Каждый набор состоит из $$$7$$$ строк, каждая содержит $$$7$$$ символов. Каждый из этих символов либо $$$\texttt{W}$$$, либо $$$\texttt{B}$$$, обозначая белую или черную клетку соответственно.
Для каждого набора входных данных выведите одно целое число — минимальное количество операций, необходимых для того, чтобы гарантировать, что нет черных клеток, у которых все четыре диагональных соседа также черные.
4WWWWWWWWWWWBBBWWWWWBWWWBBBBBWWWBWWWWWBBBWWWWWWWWWWWWWWWWWWWWWWWWBBBBBWWBBBBBWWBBBBBWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWBBBBBWBBBBBBBBBBBBBBWWWWWWWBBBBBBBBBBBBBBBBBBBBB
1 2 0 5
Первый набор входных данных изображен в условии.
Второй набор входных данных изображен ниже:
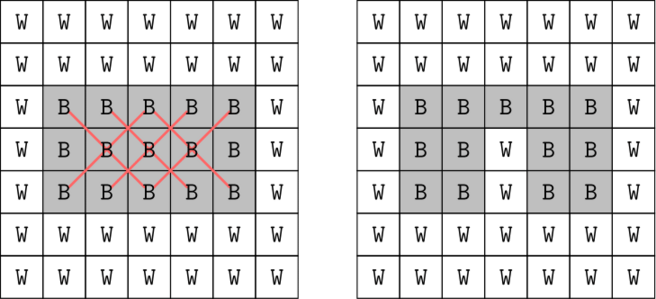
В третьем наборе входных данных поле уже удовлетворяет условию.
| Название |
|---|




