| Codeforces Round 926 (Div. 2) |
|---|
| Закончено |
Пройдя все трудности и невзгоды, Саша наконец решил жениться на своей девушке. Для этого нужно подарить ей обручальное кольцо. Однако его девушке не нравятся подобные романтические жесты, но нравятся бинарные деревья поиска$$$^{\dagger}$$$. Поэтому Саша решил ей подарить такое дерево.
Проведя немало времени на свадебных сайтах для программистов, он нашел идеальное бинарное дерево поиска с корнем в вершине $$$1$$$. В нём значение в вершине $$$v$$$ равно $$$val_v$$$.
Но спустя некоторое время он забыл значения в некоторых вершинах. Пытаясь вспомнить найденное дерево, Саша задался вопросом — сколько существует бинарных деревьев поиска, которые он мог найти на сайте, если известно, что значения во всех вершинах являются целыми числами и принадлежат отрезку $$$[1, C]$$$. Поскольку это число может быть очень большим, выведите его по модулю $$$998\,244\,353$$$.
$$$^{\dagger}$$$Бинарным деревом поиска называется корневое бинарное дерево, у которого для любой вершины $$$x$$$ выполняется свойство: значения всех вершин в левом поддереве вершины $$$x$$$ (если оно существует) меньше или равны значению в вершине $$$x$$$ и значения всех вершин в правом поддереве вершины $$$x$$$ (если оно существует) больше или равны значению в вершине $$$x$$$.
Каждый тест состоит из нескольких наборов входных данных. Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^5$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит два целых числа $$$n$$$ и $$$C$$$ ($$$2 \leq n \leq 5 \cdot 10^5$$$, $$$1 \leq C \leq 10^9$$$) — количество вершин в дереве и максимально допустимое значение в вершине.
Следующие $$$n$$$ строк описывают вершины дерева. $$$i$$$-я из них содержит три целых числа $$$L_i, R_i$$$ и $$$val_i$$$ ($$$-1 \le L_i, R_i \le n$$$, $$$-1 \le val_i \le C$$$, $$$L_i, R_i, val_i \ne 0$$$) — номер левого сына, правого сына и значение в $$$i$$$-й вершине, соответственно. Если $$$L_i = -1$$$, то у $$$i$$$-й вершины нет левого сына. Если $$$R_i = -1$$$, то у $$$i$$$-й вершины нет правого сына. Если $$$val_i = -1$$$, то значение в $$$i$$$-й вершине неизвестно.
Гарантируется, что существует хотя бы одно подходящее бинарное дерево поиска.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$5 \cdot 10^5$$$.
Для каждого набора входных данных выведите единственное целое число — количество подходящих бинарных деревьев поиска по модулю $$$998\,244\,353$$$.
35 52 3 -1-1 -1 24 -1 3-1 5 -1-1 -1 -13 692 3 47-1 -1 13-1 -1 693 32 3 -1-1 -1 -1-1 -1 -1
4 1 10
В первом наборе входных данных, бинарное дерево поиска имеет следующий вид:
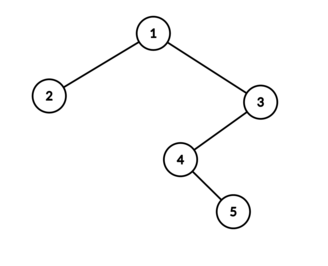
Тогда возможными значениями в вершинах являются: $$$[2, 2, 3, 2, 2]$$$, $$$[2, 2, 3, 2, 3]$$$, $$$[2, 2, 3, 3, 3]$$$ и $$$[3, 2, 3, 3, 3]$$$.
Во втором наборе входных данных значения во всех вершинах известны, поэтому существует единственное подходящее бинарное дерево поиска.
| Название |
|---|




