| Codeforces Round 941 (Div. 1) |
|---|
| Закончено |
У вас есть полоска бумаги с бинарной строкой $$$s$$$ длины $$$n$$$. Вы можете сложить бумагу между любой парой соседних цифр.
Последовательность складок считается допустимой, если после складок все символы, находящиеся друг над другом или под другим, совпадают. Обратите внимание, что все складки делаются одновременно, поэтому символы не обязательно должны совпадать между складками.
Например, вот допустимые складки для $$$s = \mathtt{110110110011}$$$ и $$$s = \mathtt{01110}$$$:
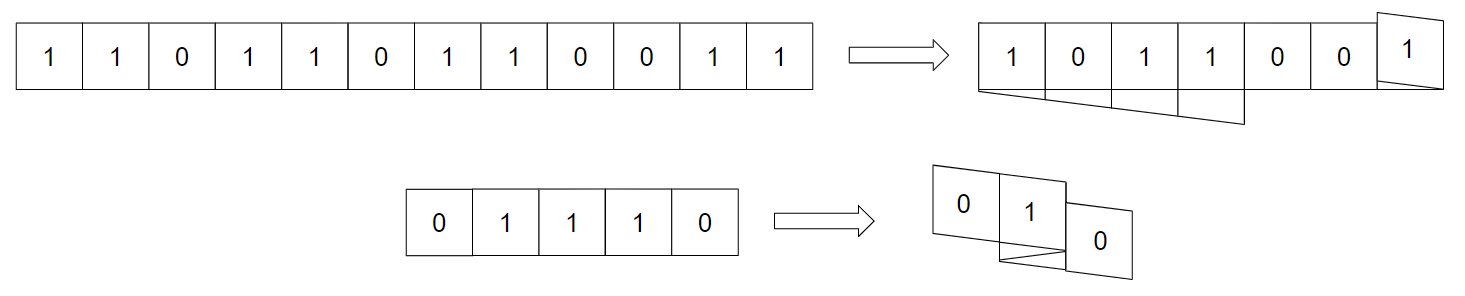
Длина сложенной полоски — это длина, видимая сверху после всех складок. Таким образом, для двух приведенных выше примеров после указанных выше складок длины будут равны $$$7$$$ и $$$3$$$ соответственно.
Обратите внимание, что для приведенной выше складки для $$$s = \mathtt{01110}$$$, если бы мы сделали любую из двух складок по отдельности, это была бы недопустимая последовательность складок. Однако, поскольку мы не проверяем допустимость до тех пор, пока все складки не будут сделаны, эта последовательность складок допустима.
После выполнения последовательности допустимых складок, какова минимальная длина полоски, которую вы можете получить?
Первая строка ввода содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество тестов. Затем следует описание тестов.
Первая строка каждого теста содержит одно целое число $$$n$$$ ($$$1 \le n \le 2\cdot 10^5$$$) — размер полоски.
Вторая строка каждого теста содержит строку $$$s$$$ из $$$n$$$ символов '0' и '1' — описание цифр на полоске.
Гарантируется, что сумма $$$n$$$ по всем тестам не превышает $$$2\cdot 10^5$$$.
Для каждого теста выведите одно целое число — минимально возможную длину полоски после допустимой последовательности складок.
66101101101211011011001150111041111201
3 1 3 3 1 2
Для первого примера одной из оптимальных последовательностей складок является складывание полоски посередине, что приводит к полоске длиной 3.
Третий и четвертый примеры соответствуют изображениям выше. Обратите внимание, что складка, показанная выше для $$$s = \mathtt{110110110011}$$$, не является минимальной по длине.
| Название |
|---|




