| Codeforces Round 949 (Div. 2) |
|---|
| Закончено |
Черепаха только что получила $$$n$$$ отрезков и последовательность $$$a_1, a_2, \ldots, a_n$$$. $$$i$$$-й отрезок представляет собой $$$[l_i, r_i]$$$.
Черепаха создаст неориентированный граф $$$G$$$. Если отрезок $$$i$$$ и отрезок $$$j$$$ пересекаются, то Черепаха добавит неориентированное ребро между $$$i$$$ и $$$j$$$ с весом $$$|a_i - a_j|$$$, для каждого $$$i \ne j$$$.
Черепаха хочет, чтобы вы вычислили сумму весов рёбер минимального остовного дерева графа $$$G$$$, или сообщили, что у графа $$$G$$$ нет остовного дерева.
Мы говорим, что два отрезка $$$[l_1, r_1]$$$ и $$$[l_2, r_2]$$$ пересекаются тогда и только тогда, когда $$$\max(l_1, l_2) \le \min(r_1, r_2)$$$.
Каждый тест содержит несколько тестовых случаев. Первая строка содержит количество тестов $$$t$$$ ($$$1 \le t \le 10^5$$$). Далее следует описание тестов.
Первая строка каждого теста содержит одно целое число $$$n$$$ ($$$2 \le n \le 5 \cdot 10^5$$$) — количество отрезков.
$$$i$$$-я из следующих $$$n$$$ строк содержит три целых числа $$$l_i, r_i, a_i$$$ ($$$1 \le l_i \le r_i \le 10^9, 1 \le a_i \le 10^9$$$) — $$$i$$$-й отрезок и $$$i$$$-й элемент последовательности.
Гарантируется, что сумма $$$n$$$ по всем тестовым случаям не превышает $$$5 \cdot 10^5$$$.
Для каждого теста выведите одно целое число — сумму весов рёбер минимального остовного дерева графа $$$G$$$. Если у графа $$$G$$$ нет остовного дерева, выведите $$$-1$$$.
451 7 32 4 63 5 56 7 93 4 452 7 31 3 64 5 56 7 91 1 441 4 31 2 13 4 51 4 431 3 12 3 34 5 8
9 13 4 -1
В первом тесте граф $$$G$$$ выглядит следующим образом:

Одно из минимальных остовных деревьев $$$G$$$ выглядит следующим образом:

Сумма весов рёбер минимального остовного дерева равна $$$9$$$.
Во втором тесте граф $$$G$$$ выглядит следующим образом:

$$$G$$$ уже является деревом, и сумма весов дерева равна $$$13$$$.
В третьем тесте граф $$$G$$$ выглядит следующим образом:
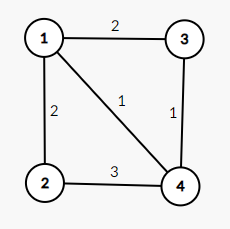
В четвертом тесте граф $$$G$$$ выглядит следующим образом:

Легко видеть, что $$$G$$$ не связан, поэтому у $$$G$$$ нет остовного дерева.
| Название |
|---|




