| Codeforces Round 127 (Div. 1) |
|---|
| Закончено |
Рассмотрим некоторую квадратную матрицу A со стороной n, состоящую из нулей и единиц. Пронумеруем ее строки от 1 до n сверху вниз и столбцы от 1 до n слева направо. Элемент матрицы, находящийся на пересечении i-ой строки и j-го столбца, будем обозначать Ai, j.
Назовем матрицу A четкой, если никакие две клетки, в которых стоят единицы, не имеют общей стороны.
Назовем матрицу A симметричной, если она в точности совпадает с матрицами, образованными из нее горизонтальным и/или вертикальным отражением. Формально, для любой пары (i, j) (1 ≤ i, j ≤ n) оба следующих условия должны быть выполнены: Ai, j = An - i + 1, j и Ai, j = Ai, n - j + 1.
Остротой матрицы A назовем количество единиц в ней.
Ваша задача — по заданному числу x найти минимальное натуральное число n такое, что существует четкая симметричная матрица A со стороной n и остротой x.
В единственной строке записано целое число x (1 ≤ x ≤ 100) — требуемая острота матрицы.
Выведите единственное число — искомое значение n.
4
3
9
5
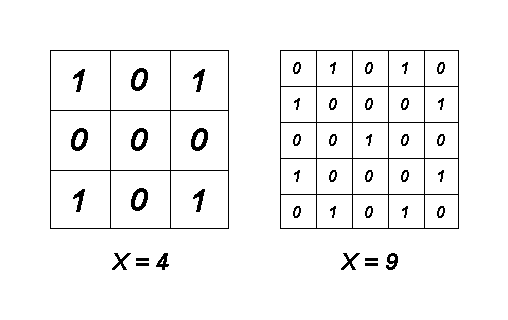
Соответствующие примерам матрицы приведены на рисунке:
| Название |
|---|




