| Abbyy Cup 2.0 - Финал (неоф. трансляция) |
|---|
| Закончено |
Умный Бобер из ABBYY в очередной раз удивляет! Он разработал новое вычислительное устройство, которое назвал «Бобриный вычислитель 1.0». Оно является весьма специфическим и планируется для использования в различных научных задачах.
Для тестирования Умный Бобер пригласил n ученых, пронумерованных от 1 до n. i-ый ученый принес ki вычислительных задач для устройства, разработанного Умным Бобром из ABBYY. Задачи i-го ученого пронумерованы от 1 до ki, причем они должны выполняться последовательно в описанном порядке, так как выполнение каждой задачи существенно зависит от результатов выполнения предыдущих.
Каждую задачу каждого из n ученых характеризует одно целое число ai, j, где i (1 ≤ i ≤ n) — номер ученого, j (1 ≤ j ≤ ki) — номер задачи, ai, j –– количество единиц ресурсов вычислительного устройства, требуемое для выполнения данной задачи.
Разработанное Умным Бобром вычислительное устройство обладает некоторыми особенностями. Задачи на нем выполняются последовательно одна за другой. После завершения выполнения некоторой задачи и перед выполнением следующей задачи происходит выделение либо освобождение ресурсов вычислительного устройства.
Самой затратной операцией для вычислительного устройства, разработанного Умным Бобром, является освобождение ресурсов, которое работает существенно медленнее выделения. Поэтому желательно, чтобы каждая следующая задача для вычислительного устройства требовала ресурсов не меньше, чем предыдущая.
Вам дана информация о задачах, предложенных учеными для тестирования. Вам требуется расположить эти задачи в таком порядке, чтобы число соседних «плохих» пар задач в этом списке было минимально возможным. Будем называть две подряд идущие задачи в этом списке «плохой» парой, если задача, которая выполняется раньше, требует большего количества ресурсов. Не забудьте, что задачи одного и того же ученого должны выполняться в строго определенном порядке.
В первой строке содержится целое число n — количество ученых. В каждой из следующих n строк в целях уменьшения объёма входных данных содержатся пять целых чисел ki, ai, 1, xi, yi, mi (0 ≤ ai, 1 < mi ≤ 109, 1 ≤ xi, yi ≤ 109) — количество задач i-го ученого, требуемое количество ресурсов для первой задачи, а также три параметра для генерации последующих значений ai, j. Для всех j от 2 до ki, включительно, значение ai, j следует вычислить по формуле ai, j = (ai, j - 1 * xi + yi) mod mi, где a mod b — операция взятия остатка от деления числа a на число b.
Для получения полного балла за первую группу тестов достаточно решить задачу при n = 2, 1 ≤ ki ≤ 2000.
Для получения полного балла за вторую группу тестов достаточно решить задачу при n = 2, 1 ≤ ki ≤ 200000.
Для получения полного балла за третью группу тестов достаточно решить задачу при 1 ≤ n ≤ 5000, 1 ≤ ki ≤ 5000.
В первой строке выведите единственное число — количество «плохих» пар в оптимальном расположении.
Если общее количество задач не превышает 200000, выведите также 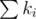 строк — оптимальное расположение задач. В каждой из этих строк выведите два целых числа, разделённых одиночным пробелом — требуемое число ресурсов для задачи и номер ученого, предложившего эту задачу, соответственно. Ученые пронумерованы от 1 до n в порядке ввода.
строк — оптимальное расположение задач. В каждой из этих строк выведите два целых числа, разделённых одиночным пробелом — требуемое число ресурсов для задачи и номер ученого, предложившего эту задачу, соответственно. Ученые пронумерованы от 1 до n в порядке ввода.
2
2 1 1 1 10
2 3 1 1 10
0
1 1
2 1
3 2
4 2
2
3 10 2 3 1000
3 100 1 999 1000
2
10 1
23 1
49 1
100 2
99 2
98 2
В первом примере n = 2, k1 = 2, a1, 1 = 1, a1, 2 = 2, k2 = 2, a2, 1 = 3, a2, 2 = 4. У нас два ученых, у каждого из которых две вычислительные задачи. Задачи первого требуют 1 и 2 единицы ресурсов, а задачи второго — 3 и 4 единицы ресурсов. Выпишем все возможные варианты для порядка вычислений (для каждой задачи указаны только требуемые для нее ресурсы): (1, 2, 3, 4), (1, 3, 2, 4), (3, 1, 2, 4), (1, 3, 4, 2), (3, 4, 1, 2), (3, 1, 4, 2).
В последовательности задач (1, 3, 2, 4) одна «плохая» пара (3 и 2), в (3, 1, 4, 2) — две «плохие» пары (3 и 1, 4 и 2), а в (1, 2, 3, 4) нет «плохих» пар.
| Название |
|---|




