| Codeforces Round 144 (Div. 1) |
|---|
| Закончено |
У Джона Доу есть таблица размером n × m. Джон Доу может нарисовать в некоторых ячейках таблицы точки, не более одной точки в одной ячейке таблицы. С помощью таких операций Джон Доу хочет добиться того, чтобы в любой квадратной подтаблице размера n × n количество точек было в точности равно k.
Джону Доу стало интересно, сколькими различными способами можно заполнить эту таблицу точками так, чтобы описанное условие выполнялось. Поскольку это число может быть очень велико, Джон Доу просит узнать его остаток от деления на 1000000007 (109 + 7).
Считайте, что Джон всегда рисует точку строго в центре некоторой ячейки. Два способа заполнения таблицы точками считаются различными, если существует ячейка таблицы, в которой в одном способе нарисована точка, а в другом — нет.
В единственной строке через пробел записаны целые числа n, m, k (1 ≤ n ≤ 100; n ≤ m ≤ 1018; 0 ≤ k ≤ n2) — количество строк в таблице, количество столбцов в таблице и количество точек, которое должно быть в каждом квадрате.
Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d.
В единственной строке выведите целое число — остаток от деления описанного количества способов на 1000000007 (109 + 7).
5 6 1
45
Рассмотрим первый тестовый пример:
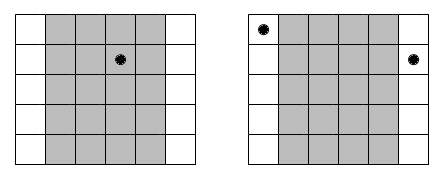
| Название |
|---|




