| Codeforces Round 148 (Div. 1) |
|---|
| Закончено |
Последовательность неотрицательных целых чисел a1, a2, ..., an длины n называется шерстяной последовательностью тогда и только тогда, когда существует два целых числа l и r (1 ≤ l ≤ r ≤ n), таких, что  . Иными словами, шерстяная последовательность содержит подпоследовательность из последовательных элементов, xor которых равен 0.
. Иными словами, шерстяная последовательность содержит подпоследовательность из последовательных элементов, xor которых равен 0.
Выражение 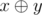 означает применение побитовой операции xor к числам x и y. Данная операция существует во всех современных языках программирования, например, в языках C++ и Java она обозначена как «^», в Pascal — как «xor».
означает применение побитовой операции xor к числам x и y. Данная операция существует во всех современных языках программирования, например, в языках C++ и Java она обозначена как «^», в Pascal — как «xor».
В этой задаче Вас попросили подсчитать количество последовательностей, составленных из n чисел от 0 до 2m - 1, не являющихся шерстяными последовательностями. Выведите это количество по модулю 1000000009 (109 + 9).
Единственная строка входных данных содержит через пробел целые числа n и m (1 ≤ n, m ≤ 105).
В единственной строке выходных данных выведите искомое количество последовательностей по модулю 1000000009 (109 + 9).
3 2
6
Последовательности длины 3, сделанные из целых чисел 0, 1, 2 и 3, не являющиеся шерстяными последовательностями, таковы: (1, 3, 1), (1, 2, 1), (2, 1, 2), (2, 3, 2), (3, 1, 3) и (3, 2, 3).
| Название |
|---|




