Две деревни разделены рекой, которая течет с севера на юг. Жители деревень хотят построить мост через реку, чтобы можно было проще перемещаться между деревнями.
Берега реки можно считать вертикальными прямыми x = a и x = b (0 < a < b).
Западная деревня находится в степи в точке O = (0, 0). От деревни к реке ведут n тропинок, которые заканчиваются в точках Ai = (a, yi). Жители этой деревни простодушны и прямолинейны, поэтому и тропинки представляют собой отрезки прямых.
Жители восточной деревни скрытны и хитры. Их деревня находится в лесу на восточном берегу реки, но точное ее положение неизвестно. От этой деревни к реке ведут m извилистых тропинок, которые заканчиваются в точках Bi = (b, y'i). Длины всех этих тропинок известны, длина тропинки, ведущей от восточной деревни в точку Bi, равна li.
Жители деревень хотят выбрать ровно одну из точек на левом берегу реки Ai, ровно одну из точек на правом берегу Bj и соединить их прямолинейным мостом так, чтобы итоговое расстояние между деревнями (сумма |OAi| + |AiBj| + lj, где |XY| — евклидово расстояние между точками X и Y) было минимальным. Евклидово расстояние между точками (x1, y1) и (x2, y2) равно 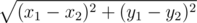 .
.
Помогите им и найдите искомую пару точек.
В первой строке записаны целые числа n, m, a, b (1 ≤ n, m ≤ 105, 0 < a < b < 106).
Во второй строке записаны n целых чисел в возрастающем порядке: i-ое из них определяет координату точки Ai и равно yi (|yi| ≤ 106).
В третьей строке записаны m целых чисел в возрастающем порядке: i-ое из них определяет координату точки Bi и равно y'i (|y'i| ≤ 106).
В четвертой строке записаны еще m целых чисел: i-ое из них определяет длину тропинки, соединяющей восточную деревню и точку Bi, и равно li (1 ≤ li ≤ 106).
Гарантируется, что существует такая точка C с абсциссой не менее b, что |BiC| ≤ li для всех i (1 ≤ i ≤ m). Гарантируется, что никакие две точки Ai не совпадают. Гарантируется, что никакие две точки Bi не совпадают.
Выведите два целых числа — номера точек на левом (западном) и правом (восточном) берегу соответственно, между которыми нужно построить мост. Можете считать, что точки на западном берегу пронумерованы целыми числами от 1 до n в том порядке, в котором они даны во входных данных. Аналогично точки на восточном берегу пронумерованы целыми числами от 1 до m в том порядке, в котором даны во входных данных.
Если существует несколько решений — выведите любое. Решение будет засчитано, если итоговая длина пути будет отличаться от ответа жюри не более чем на 10 - 6 по абсолютному или относительному значению.
3 2 3 5
-2 -1 4
-1 2
7 3
2 2
| Название |
|---|




