| Codeforces Round 165 (Div. 1) |
|---|
| Закончено |
Эмускальд считает себя мастером алгоритмов по нахождению потока. Он только что завершил самую искусную из всех своих программ: она вычисляет максимальный поток в неориентированном графе. Граф состоит из n вершин и m ребер. Вершины пронумерованы от 1 до n. Вершины 1 и n — исток и сток, соответственно.
Однако, его алгоритм максимального потока, похоже, немного неисправен: для каждого ребра он находит только величину потока, протекающего по этому ребру, но не направление, в котором течет поток. Помогите ему для каждого ребра найти направление, в котором должен протекать поток по этому ребру, чтобы в итоге получился корректный максимальный поток.
Более формально: дан неориентированный граф, в котором для каждого неориентированного ребра (ai, bi) задана величина ci. Вы должны ориентировать все ребра так, чтобы выполнялись следующие условия:
- для каждой вершины v (1 < v < n), сумма ci входящих ребер равняется сумме ci исходящих ребер;
- вершина номер 1 не имеет входящих ребер;
- полученный ориентированный граф не имеет циклов.
Первая строка входных данных содержит два целых числа через пробел n и m (2 ≤ n ≤ 2·105, n - 1 ≤ m ≤ 2·105), количество вершин и ребер в графе. Каждая из следующих m строк содержит три целых числа ai, bi и ci (1 ≤ ai, bi ≤ n, ai ≠ bi, 1 ≤ ci ≤ 104) через пробел, которые обозначают неориентированное ребро от ai до bi, по которому протекает в некотором направлении ci единиц потока.
Гарантируется, что не существует двух ребер, соединяющих одни и те же вершины; данный граф связный; решение всегда существует.
Выведите m строк, в каждой строке должно быть по целому числу di, равному 0, если направление i-го ребра равняется ai → bi (поток протекает от вершины ai к вершине bi), и равному 1 в противном случае. Считайте, что ребра пронумерованы от 1 до m в том порядке, в котором они заданы во входных данных.
Если существует несколько решений, выведите любое из них.
3 3
3 2 10
1 2 10
3 1 5
1
0
1
4 5
1 2 10
1 3 10
2 3 5
4 2 15
3 4 5
0
0
1
1
0
В первом тестовом примере 10 единиц потока проходят по пути 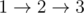 , а 5 единиц потока проходят прямо от истока к стоку:
, а 5 единиц потока проходят прямо от истока к стоку: 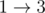 .
.
| Название |
|---|




