| Codeforces Round 192 (Div. 2) |
|---|
| Закончено |
В одной стране есть n городов. Изначально в этой стране нет дорог. Но вот, однажды король решает построить дороги, соединяющие пары городов. По дорогам можно путешествовать в любую сторону. Король хочет построить дороги так, чтобы можно было добраться из любого города в любой другой, проехав не более двух дорог. Также дано m пар городов — между этими парами городов дороги строить нельзя.
Ваша задача — построить как можно меньше дорог так, чтобы вышеперечисленные условия выполнялись. Ограничения гарантируют, что это возможно всегда.
Первая строка содержит два целых числа, n и m 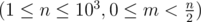 .
.
Затем следует m строк, каждая строка состоит из двух целых чисел, ai и bi (1 ≤ ai, bi ≤ n, ai ≠ bi), показывающих, что нельзя строить дорогу между городами ai и bi. Считайте, что города пронумерованы от 1 до n.
Гарантируется, что каждая пара городов упоминается во входных данных ровно один раз.
В первой строке выведите целое число s: наименьшее количество дорог, которые надо построить. Затем следует вывести s строк, по два целых числа ai и bi (1 ≤ ai, bi ≤ n, ai ≠ bi) в каждой, означающих, что надо построить дорогу между городами ai и bi.
Если существует несколько решений, можно выводить любое.
4 1
1 3
3
1 2
4 2
2 3
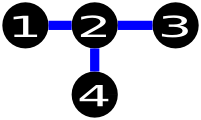
Ниже показано одно из возможных решений тестового примера:
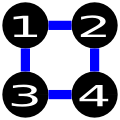
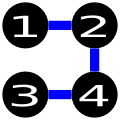
Примеры неправильных решений:
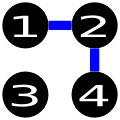
| Название |
|---|




