| Codeforces Round 210 (Div. 1) |
|---|
| Закончено |
Левко сильно любит массив a1, a2, ... , an, состоящий из целых чисел. Именно поэтому Левко много играет с массивом a, выполняя различные операции с ним. Каждая операция, которую выполняет Левко, имеет один из двух следующих типов:
- Увеличить все элементы от li до ri на di. Другими словами выполнить присвоения aj = aj + di для всех j, удовлетворяющих неравенству: li ≤ j ≤ ri.
- Найти максимум элементов от li до ri. То есть посчитать значение
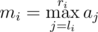 .
.
К большому сожалению, недавно Левко потерял свой массив. К счастью, у Левко остались записи всех операций, которые он выполнял с массивом a. Помогите Левко — по записям операций найдите хотя бы один подходящий массив. Результаты всех операций для найденного массива должны совпадать с результатами из записей. Левко точно помнит, что в его массиве все числа не превосходили 109 по модулю, поэтому он просит вас найти именно такой массив.
В первой строке записаны два целых числа n и m (1 ≤ n, m ≤ 5000) — размер массива и количество операций в записях Левко соответственно.
Следующие m строк описывают операции, i-ая строка описывает i-ую операцию. Первое число в i-ой строке — целое число ti (1 ≤ ti ≤ 2), которое обозначает тип операции. Если ti = 1, то далее следуют три целых числа li, ri и di (1 ≤ li ≤ ri ≤ n, - 104 ≤ di ≤ 104) — описание операции первого типа. Если ti = 2, то далее следуют три целых числа li, ri и mi (1 ≤ li ≤ ri ≤ n, - 5·107 ≤ mi ≤ 5·107) — описание операции второго типа.
Операции заданы в том порядке, в котором Левко выполнял их со своим массивом.
В первой строке выведите «YES» (без кавычек), если решение существует, и «NO» (без кавычек) в противном случае.
Если решение все-таки существует, то во второй строке выведите n целых чисел a1, a2, ... , an (|ai| ≤ 109) — найденный массив.
4 5
1 2 3 1
2 1 2 8
2 3 4 7
1 1 3 3
2 3 4 8
YES
4 7 4 7
4 5
1 2 3 1
2 1 2 8
2 3 4 7
1 1 3 3
2 3 4 13
NO
| Название |
|---|




