| Codeforces Round 226 (Div. 2) |
|---|
| Закончено |
Недавно медведь начал изучать структуры данных и столкнулся со следующей задачей.
Задана последовательность целых чисел x1, x2, ..., xn длины n и m запросов, каждый из которых характеризуется двумя целыми числами li, ri. Обозначим за f(p) — количество таких индексов k, что xk делится на p. Ответом на запрос li, ri является сумма: 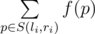 , где S(li, ri) — множество простых чисел из отрезка [li, ri] (обе границы включаются в отрезок).
, где S(li, ri) — множество простых чисел из отрезка [li, ri] (обе границы включаются в отрезок).
Помогите медведю справиться с этой задачей.
В первой строке записано целое число n (1 ≤ n ≤ 106). Во второй строке записаны n целых чисел x1, x2, ..., xn (2 ≤ xi ≤ 107). Числа не обязательно различные.
В третьей строке записано целое число m (1 ≤ m ≤ 50000). В каждой из m следующих строк записана пара целых чисел через пробел li и ri (2 ≤ li ≤ ri ≤ 2·109) — числа, характеризующие текущий запрос.
Выведите m целых чисел — ответы на запросы в порядке появления запросов во входных данных.
6
5 5 7 10 14 15
3
2 11
3 12
4 4
9
7
0
7
2 3 5 7 11 4 8
2
8 10
2 123
0
7
Рассмотрим первый тестовый пример. Всего в первом примере 3 запроса.
- Поступает первый запрос l = 2, r = 11. Нужно посчитать f(2) + f(3) + f(5) + f(7) + f(11) = 2 + 1 + 4 + 2 + 0 = 9.
- Поступает второй запрос l = 3, r = 12. Нужно посчитать f(3) + f(5) + f(7) + f(11) = 1 + 4 + 2 + 0 = 7.
- Поступает третий запрос l = 4, r = 4. Так как на этом промежутке нет простых чисел, то сумма равна 0.
| Название |
|---|




