| Codeforces Round 233 (Div. 1) |
|---|
| Закончено |
Пользователь ainta любит деревья. В этот раз он собирается построить неориентированное дерево, состоящее из n вершин, пронумерованных целыми числами от 1 до n. Дерево — взвешенное, то есть каждое ребро дерева имеет некоторый целочисленный вес.
Также у юноши есть массив t: t[1], t[2], ..., t[n]. Сперва все элементы массива инициализируются значением 0. Затем для каждого ребра, соединяющего вершины u и v (u < v) дерева с весом c, ainta добавляет значение c к элементам t[u], t[u + 1], ..., t[v - 1], t[v] массива t.
Обозначим суммарный вес ребер на кратчайшем пути от вершины u до v записью d(u, v). Пользователь ainta называет пару целых чисел x, y (1 ≤ x < y ≤ n) хорошей тогда и только тогда, когда d(x, y) = t[x] + t[x + 1] + ... + t[y - 1] + t[y].
Пользователь ainta хочет получить не меньше 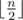 хороших пар, но у него не получается построить соответствующее дерево. Помогите ainta найти такое дерево.
хороших пар, но у него не получается построить соответствующее дерево. Помогите ainta найти такое дерево.
Первая строка содержит единственное целое число n (5 ≤ n ≤ 105).
Выведите n - 1 строк, содержащих описание ребер: i-я строка должна содержать три целых числа через пробел ui, vi, ci (1 ≤ ui < vi ≤ n; 1 ≤ ci ≤ 105) — две вершины, соединенные ребром дерева, и вес этого ребра.
Дальше выведите 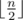 строк, содержащих хорошие пары. В k-й строке должны быть записаны два целых числа через пробел, xk и yk (1 ≤ xk < yk ≤ n). Конечно же, xk, yk должны образовывать хорошую пару. Все пары должны быть различны — иными словами, для всех j, k
строк, содержащих хорошие пары. В k-й строке должны быть записаны два целых числа через пробел, xk и yk (1 ≤ xk < yk ≤ n). Конечно же, xk, yk должны образовывать хорошую пару. Все пары должны быть различны — иными словами, для всех j, k 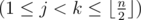 , должно выполняться условие xj ≠ xk или yj ≠ yk.
, должно выполняться условие xj ≠ xk или yj ≠ yk.
Если существует несколько правильных ответов, разрешается вывести любой из них.
7
1 4 1
1 2 2
2 3 5
3 5 3
2 6 2
6 7 3
4 5
5 6
5 7
⌊x⌋ — это наибольшее целое число, не превышающее x.
Вы можете найти определение дерева по следующей ссылке: http://ru.wikipedia.org/wiki/Дерево_(теория_графов)
Также вы можете найти определение кратчайшего пути по следующей ссылке: http://ru.wikipedia.org/wiki/Задача_о_кратчайшем_пути
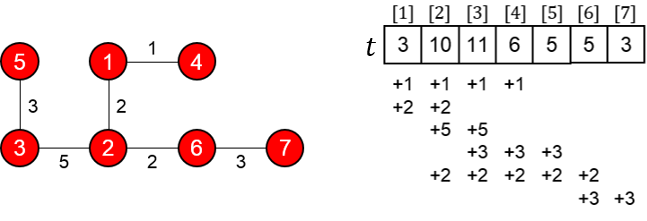
Дерево и массив t в тестовом примере выглядят следующим образом:
| Название |
|---|




