| Codeforces Round 248 (Div. 2) |
|---|
| Закончено |
Рюко фантастически рассеянная девушка, она порой забывает даже то, что вот-вот произошло. Чтобы ничего не упустить, девушка везде берет с собой блокнот под названием Блокнот памяти Рюко. Все, что она видит и слышит, она записывает в этот блокнот.
Хотя Рюко все забывает, она родилась с великолепными мыслительными способностями. С другой стороны, качество рассуждений во многом зависит от имеющейся информации, иными словами, от памяти. И вот девушка листает вой блокнот каждый раз, когда над чем-то рассуждает — а это серьезная работа.
В блокноте Рюко n страниц, пронумерованных от 1 до n. Чтобы облегчить себе жизнь (и эту задачу), мы считаем, что для перехода со страницы x на страницу y надо перелистнуть |x - y| страниц. Чтобы сделать некоторое рассуждение, Рюко нужно иметь ввиду m фактов, i-й факт написан на странице ai. Факты следует читать из блокнота по порядку, в таком случае Рюко надо пролистать 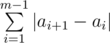 станиц, чтобы прочитать все факты.
станиц, чтобы прочитать все факты.
Рюко хочет уменьшить количество пролистываемых страниц. Для достижения этой цели девушка может скопировать всю информацию со страницы x на страницу y (1 ≤ x, y ≤ n) блокнота. А затем заменить все элементы в последовательности a, равные x, на y. Обратите внимание, что x может равняться y, в таком случае никаких перемен не происходит.
Пожалуйста, скажите Рюко, какое минимальное количество страниц ей придется перелистнуть, чтобы прочитать все факты, если она может применить описанную операцию не более одного раза перед чтением. Обратите внимание, что ответ на задачу может превысить 32-битное целое число.
В первой строке записано два целых числа, n и m (1 ≤ n, m ≤ 105).
В следующей строке записано m целых чисел, разделенных пробелами: a1, a2, ..., am (1 ≤ ai ≤ n).
Выведите единственное целое число — минимальное количество переворачиваемых страниц.
4 6
1 2 3 4 3 2
3
10 5
9 4 3 8 8
6
В первом примере оптимальное решение — записать все со страницы 4 на страницу 3, тогда последовательность a станет равна {1, 2, 3, 3, 3, 2}, таким образом, количество переворачиваемых Рюко страниц равно |1 - 2| + |2 - 3| + |3 - 3| + |3 - 3| + |3 - 2| = 3.
Во втором примере оптимальное решение достигается копированием информации со станицы 9 на страницу 4.
| Название |
|---|




