| Codeforces Round 254 (Div. 1) |
|---|
| Закончено |
DZY любит физику, больше всего ему нравится считать плотность.
Плотность есть почти у всего, даже у графа. Определим плотность неориентированного графа, вершины и ребра которого имеют некоторые значения, следующим образом:
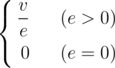
Как-то раз DZY раздобыл граф G. Теперь он хочет найти связный порожденный подграф G' данного графа с максимальной плотностью.
Порожденный подграф G'(V', E') графа G(V, E) — это граф, удовлетворяющий условиям:
-
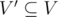 ;
; - ребро
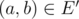 тогда и только тогда, когда
тогда и только тогда, когда 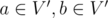 , а ребро
, а ребро 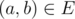 ;
; - значение ребра в G' равняется значению соответствующего ребра в G, аналогичное утверждение верно и для вершин.
Помогите DZY найти порожденный подграф с максимальной плотностью. Обратите внимание на то, что выбранный вами порожденный подграф должен быть связанным.

В первой строке записано два целых числа через пробел, n (1 ≤ n ≤ 500), 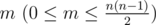 . Целое число n обозначает количество вершин графа G, m обозначает количество ребер.
. Целое число n обозначает количество вершин графа G, m обозначает количество ребер.
Во второй строке записано n целых чисел через пробел xi (1 ≤ xi ≤ 106), где xi обозначает значение i-й вершины. Считайте, что вершины графа пронумерованы от 1 до n.
В каждой из следующих m строк записано по три целых числа через пробел ai, bi, ci (1 ≤ ai < bi ≤ n; 1 ≤ ci ≤ 103), обозначающих ребро между вершинами ai и bi со значением ci. Граф не имеет кратных ребер.
Выведите действительное число, обозначающее ответ, с абсолютной или относительной погрешностью не более 10 - 9.
1 0
1
0.000000000000000
2 1
1 2
1 2 1
3.000000000000000
5 6
13 56 73 98 17
1 2 56
1 3 29
1 4 42
2 3 95
2 4 88
3 4 63
2.965517241379311
В первом примере можно выбрать либо пустой подграф, либо подграф с единственной вершиной 1.
Во втором примере оптимальное решение — выбрать весь граф.
| Название |
|---|




