| Codeforces Round 261 (Div. 2) |
|---|
| Закончено |
Сегодняшняя домашняя работа Пашмака — это задача на графы. Несмотря на то, что он всегда старается выполнить домашнюю работу полностью, эту задачу решить он не может. К сожалению, он не силен в теории графов. Пожалуйста, помогите ему.
Задан взвешенный ориентированный граф с n вершинами и m ребрами. Найдите длиннейший по количеству ребер путь, веса ребер в котором возрастают вдоль пути. Другими словами, у каждого ребра в пути должен быть строго больший вес, чем у предыдущего ребра пути.
Выведите длину описанного пути.
В первой строке записано два целых числа n, m (2 ≤ n ≤ 3·105; 1 ≤ m ≤ min(n·(n - 1), 3·105)). Затем следует m строк. В i-й строке записаны три целых числа через пробел: ui, vi, wi (1 ≤ ui, vi ≤ n; 1 ≤ wi ≤ 105), они обозначают, что в графе есть направленное ребро весом wi от вершины ui к вершине vi.
Гарантируется, что граф не содержит петель и кратных ребер.
Выведите единственное целое число — ответ на задачу.
3 3
1 2 1
2 3 1
3 1 1
1
3 3
1 2 1
2 3 2
3 1 3
3
6 7
1 2 1
3 2 5
2 4 2
2 5 2
2 6 9
5 4 3
4 3 4
6
В первом примере подходит любой из путей: 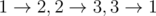 .
.
Во втором примере оптимальный путь:  .
.
В третьем примере оптимальный путь: 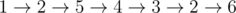 .
.
| Название |
|---|




