| Codeforces Round 278 (Div. 2) |
|---|
| Закончено |
В Киберленде есть древняя традиция держать в доме 4 коробки конфет. Количества конфет в коробках являются особенными, если их среднее арифметическое, медиана и диапазон совпадают. По определению, для набора чисел {x1, x2, x3, x4} (x1 ≤ x2 ≤ x3 ≤ x4) средним арифметическим называется 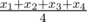 , медианой называется
, медианой называется 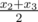 , а диапазоном — x4 - x1. Среднее арифметическое и медиана не обязательно являются целыми числами. Хорошо известно, что набор коробок особенных размеров создаёт «отладочное поле» и программы в этом поле не будут содержать баги.
, а диапазоном — x4 - x1. Среднее арифметическое и медиана не обязательно являются целыми числами. Хорошо известно, что набор коробок особенных размеров создаёт «отладочное поле» и программы в этом поле не будут содержать баги.
Например, 1, 1, 3, 3 — возможные 4 числа, которые удовлетворяют указанному условию, их среднее арифметиеское, медиана и диапазон равны 2.
У Джеффа есть 4 особенные коробки конфет. Но случилось нечто плохое! Некоторые коробки могли быть потеряны, и сейчас осталось ровно n (0 ≤ n ≤ 4) коробок. В i-й из оставшихся коробок лежит ai конфет.
Теперь Джефф хочет знать, возможно ли подобрать количества конфет в 4 - n пропавших коробках так, чтобы набор удовлетворял условию (среднее арифметическое, медиана и диапазон равны между собой)?
В первой строке ввода записано единственное целое число n (0 ≤ n ≤ 4).
В следующих n строках, записаны целые число ai, каждое из которых обозначает количество конфет в i-й коробке (1 ≤ ai ≤ 500).
Данные числа ai могут следовать в любом порядке во вводе, а не обязательно в неубывающем.
ai могли находиться на любых позициях в исходном наборе, а не обязательно на n первых позициях.
В первой строке выведите «YES», если существует хотя бы одно решение, либо выведите «NO», если решения не существует.
Если существует хотя бы одно решение, выведите ещё 4 - n строк, в каждой строке выведите число b, обозначающее количество конфет в одной из пропавших коробок.
Значения b должны удовлетворять условию 1 ≤ b ≤ 106. Гарантируется, что если существует хотя бы одно положительное целочисленное решение, вы всегда сможете найти значения b, удовлетворяющие условию. Если есть несколько решений, можно вывести любое из них.
Выводить значения b можно в любом порядке.
2
1
1
YES
3
3
3
1
1
1
NO
4
1
2
2
3
YES
В первом примере количество конфет в 4 коробках может быть равно 1, 1, 3, 3. Среднее арифметическое, медиана и диапазон равны 2.
Во втором примере невозможно найти количества пропавших конфет.
В третьем примере ни одна из коробок не пропала, и количества конфет удовлетворяют условию.
| Название |
|---|




