| Codeforces Round 315 (Div. 1) |
|---|
| Закончено |
Рихаил Мубинчик считает, что нынешнее определение простых чисел несостоятельно — они слишком сложны и непредсказуемы. Вот другое дело — палиндромные числа. И глазу приятны, и обладают рядом замечательных свойств. Помогите Рихаилу убедить научное сообщество в этом!
Напомним, что число называется простым, если оно целое, не меньше двух, и не делится ни на какое целое положительное число кроме себя и единицы.
Рихаил называет число палиндромным, если оно целое, положительное и его запись в десятичной системе счисления без ведущих нулей является палиндромом, то есть одинаково читается слева направо и справа налево.
Одна из проблем с простыми числами заключается в том, что их слишком много. Введём следующие обозначения: π(n) — количество простых чисел, не превышающих n, rub(n) — количество палиндромных чисел, не превышающих n. Рихаил хочет доказать, что простых чисел намного больше, чем палиндромных.
Он попросил вас решить следующую задачу: по заданному значению коэффициента A найти наибольшее такое n, что π(n) ≤ A·rub(n).
Ввод состоит из двух целых положительных чисел p, q — числитель и знаменатель дроби, являющейся значением коэффициента A (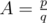 ,
, 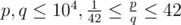 ).
).
Если наибольшее такое число существует, то вывести его. Иначе вывести "Palindromic tree is better than splay tree" (без кавычек).
1 1
40
1 42
1
6 4
172
| Название |
|---|




