| Codeforces Round 315 (Div. 1) |
|---|
| Закончено |
Вовочка недавно занялся теорией множеств. Сейчас он проходит бинарные отношения. Вы, наверное, слышали термин «отношение эквивалентности». Такие отношения очень важны во многих разделах математики. Например, равенство двух чисел является отношением эквивалентности.
Набор ρ пар (a, b) элементов некоторого множества A называется бинарным отношением на множестве A. Про два элемента a и b множества A говорят, что они находятся в отношении ρ, если пара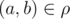 
, в таком случае пишут 
.
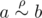Бинарное отношение является отношением эквивалентности, если:
- Оно рефлексивно (для любого a верно
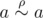); - Оно симметрично (для любых a, b верно, что если 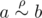, то
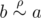); - Оно транзитивно (если 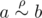и
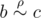, то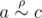 
).
Вовочка очень даже не дурак и заметил, что первое условие не нужно! Вот его «доказательство»:
Возьмём любые два элемента a и b. Если 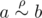, то 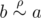(по свойству (2)), а значит 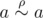(по свойству (3)).
Все очень просто, не правда ли? Однако, вы заметили, что «доказательство» Вовочки неверно, и решили предъявить ему множество примеров, доказывающих его неправоту.
Вот ваше задание: посчитайте количество бинарных отношений над множеством размера n таких, что они симметричны, транзитивны, но не являются отношениями эквивалентности (то есть не являются рефлексивными).
Так как их количество может быть очень большим (а не 0, как считает Вовочка), выведите остаток от деления их количества на 109 + 7.
В единственной строке находится одно целое число n (1 ≤ n ≤ 4000).
В единственной строке выведите ответ на задачу по модулю 109 + 7.
1
1
2
3
3
10
При n = 1 есть только одно такое отношение — пустое, т.е.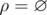 
. Иными словами, для единственного элемента x множества A выполнено 
.
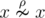При n = 2 таких отношений уже три. Пусть множество A состоит из двух элементов x и y. Тогда подходящими элементами являются 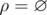, ρ = {(x, x)}, ρ = {(y, y)}. Нетрудно видеть, что три перечисленных бинарных отношения являются симметричными и транзитивными отношениями, но не являются отношениями эквивалентности.
