| Codeforces Round 322 (Div. 2) |
|---|
| Закончено |
Петя очень любит компьютерные игры. Наконец вышла игра, которую он так долго ждал!
У главного героя этой игры есть n различных навыков, каждый из которых характеризуется целым числом ai от 0 до 100. Чем больше число ai, тем лучше главный герой владеет i-м навыком. Суммарный рейтинг главного героя определяется как сумма значений 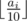 по всем i от 1 до n. Выражение ⌊ x⌋ обозначает результат округления числа x вниз к ближайшему целому числу.
по всем i от 1 до n. Выражение ⌊ x⌋ обозначает результат округления числа x вниз к ближайшему целому числу.
Пете в начале игры в качестве бонуса дали k единиц улучшений, которые он может использовать для увеличения навыков своего персонажа и его суммарного рейтинга. Используя одну единицу улучшения, Петя может увеличить любой навык главного героя ровно на один. К примеру, если a4 = 46, то после применения единицы улучшения к этому навыку, он станет равен 47. Больше 100 навык героя стать не может. Таким образом, возможно, что некоторое количество единиц улучшения останется невостребованным.
Перед вами стоит задача определить, как следует использовать единицы улучшений, чтобы максимизировать суммарный рейтинг главного героя. Использовать все единицы улучшений не обязательно.
В первой строке входных данных следуют два целых положительных числа n и k (1 ≤ n ≤ 105, 0 ≤ k ≤ 107) — количество навыков главного героя и количество единиц улучшений, имеющихся у Пети.
Во второй строке входных данных следует последовательность из n целых чисел ai (0 ≤ ai ≤ 100), где ai характеризует уровень развитости i-го навыка главного героя.
В единственной строке выходных данных должно содержаться целое неотрицательное число — максимальный суммарный рейтинг главного героя, который может получить Петя, используя k или менее единиц улучшения.
2 4
7 9
2
3 8
17 15 19
5
2 2
99 100
20
В первом тестовом примере оптимальная стратегия следующая. Петя должен улучшить первый навык до 10, потратив 3 единицы улучшения, и второй навык до 10, потратив одну единицу улучшения. Таким образом, Петя потратит все свои единицы улучшения и суммарный рейтинг главного героя станет равен 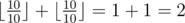 .
.
Во втором тестовом примере оптимально для Пети улучшить первый навык до 20 (при этом потратить 3 единицы улучшения) и улучшить третий навык до 20 (при этом потратить 1 единицу улучшения). Таким образом, у Пети останется 4 единицы улучшения и он сможет увеличить второй навык лишь до 19 (что не изменит суммарный рейтинг, поэтому делать это Пете необязательно). Поэтому максимально возможный суммарный рейтинг в этом примере 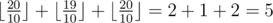 .
.
В третьем тестовом примере оптимальная стратегия Пети — увеличить первый навык до 100, потратив 1 единицу улучшения. После этого оба навыка главного героя станут равны 100, поэтому Петя не сможет потратить оставшуюся единицу улучшения. Таким образом, ответ равен 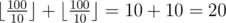 .
.
| Название |
|---|




