| Codeforces Round 335 (Div. 1) |
|---|
| Закончено |
Студент Владислав, как обычно, пришёл на экзамен по программированию, совершенно не подготовившись, и ему снова достался билет про какой-то непонятный алгоритм на графе, который абсолютно точно никогда не пригодится ему в жизни. Он попросил у сидящей рядом студентки шпаргалку по этому билету и обнаружил в ней следующее определение:
Минимальным остовным деревом T графа G называется такое дерево, что оно содержит все вершины исходного графа G, а сумма весов его рёбер — минимально возможная среди всех таких деревьев.
Владислав по привычке нарисовал граф с n вершинами и m ребрами, в котором не было петель и кратных ребер. Он нашел одно из его минимальных остовных деревьев, а потом записал для каждого ребра графа его вес, а также входит оно в найденное дерево или нет. К сожалению, бумажка, на которой был нарисован граф, исчезла, а преподаватель очень сердится и требует предоставить ему исходный граф. Помогите Владиславу придумать граф, соответствующий выписанной им информации о минимальном остовном дереве.
В первой строке записаны два целых числа n и m (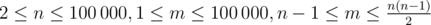
) — количество вершин и рёбер в графе.
Каждая из следующих m строк описывает ребро графа и состоит из двух чисел aj и bj (1 ≤ aj ≤ 109, bj = {0, 1}). Первое из этих чисел — это вес ребра, а второе число равно единице, если это ребро входило в минимальное остовное дерево, найденное Владиславом, и нулю, если не входило.
Гарантируется, что ровно n - 1 число из {bj} равны единице, и ровно m - n + 1 из них равны нулю.
Если Владислав ошибся, и такого графа не существует, то выведите - 1. В противном случае выведите m строк. В j-й строке выведите пару вершин (uj, vj) (1 ≤ uj, vj ≤ n, uj ≠ vj), которые должны быть соединены j-м ребром. Рёбра нумеруются в том же порядке, что и во входных данных. Граф, заданный этими ребрами, должен быть связным, не содержать петель и кратных ребер, а его ребра с bj = 1 должны задавать минимальное остовное дерево. Если существует несколько графов, удовлетворяющих условию, разрешается вывести любой.
4 5
2 1
3 1
4 0
1 1
5 0
2 4
1 4
3 4
3 1
3 2
3 3
1 0
2 1
3 1
-1
