| Good Bye 2015 |
|---|
| Закончено |
Лимак — белый медвежонок, который очень любит играть. Недавно он получил прямоугольную таблицу, состоящую из h рядов и w столбцов. Каждая клетка этой таблицы либо пустая (обозначается '.'), либо занятая (обозначается '#'). Ряды нумеруются от 1 до h сверху вниз. Столбцы нумеруются от 1 до w слева направо.
Также у Лимака есть одна доминошка, которую он хочет поместить куда-нибудь в табличку. Доминошка займёт две соседние по стороне клетки, расположенные в одной строке или в одном столбце. Обе эти клетки должны быть пустыми и находиться внутри таблицы.
Лимаку нужно больше играть и веселиться, поэтому он рассмотрит некоторые запросы. В каждом запросе он выбирает некоторый прямоугольник и задаётся вопросом: а сколькими способами можно полностью поместить имеющуюся доминошку в выбранный прямоугольник?
В первой строке записаны два целых числа h и w (1 ≤ h, w ≤ 500) — количество строк и количество столбцов в таблице, соответственно.
В следующих h строках записана таблица. В каждой строке находится строка длины w, каждый символ которой равен либо '.', либо '#', что означает пустую и занятую клетку, соответственно.
В следующей строке записано единственное число q (1 ≤ q ≤ 100 000) — количество запросов.
В каждой из следующих q строк находятся по четыре целых числа r1i, c1i, r2i, c2i (1 ≤ r1i ≤ r2i ≤ h, 1 ≤ c1i ≤ c2i ≤ w) — i-й запрос. Числа r1i и c1i определяет верхний левый угол, а числа r2i и c2i — нижний правый угол соответствующего прямоугольника.
Выведите q чисел, i-е из которых соответствует количеству способов полностью расположить доминошку внутри i-го прямоугольника.
5 8
....#..#
.#......
##.#....
##..#.##
........
4
1 1 2 3
4 1 4 1
1 2 4 5
2 5 5 8
4
0
10
15
7 39
.......................................
.###..###..#..###.....###..###..#..###.
...#..#.#..#..#.........#..#.#..#..#...
.###..#.#..#..###.....###..#.#..#..###.
.#....#.#..#....#.....#....#.#..#..#.#.
.###..###..#..###.....###..###..#..###.
.......................................
6
1 1 3 20
2 10 6 30
2 10 7 30
2 2 7 7
1 7 7 7
1 8 7 8
53
89
120
23
0
2
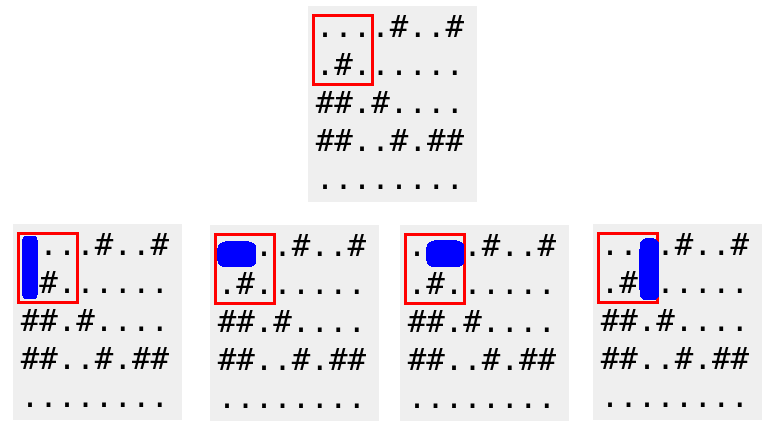
Красная рамочка на рисунке ниже соответствует первому запросу в первом примере. Существует 4 способа расположить доминошку.
| Название |
|---|




