| AIM Tech Round (Div. 1) |
|---|
| Закончено |
Однажды, сидя на лекции, студент Вася увидел, что на его парте написана строка s1s2... sn, состоящая только из букв «a», «b» и «c». Поскольку лекция была скучной, Вася решил дополнить рисунок, построив граф G, обладающий следующими свойствами:
- G имеет ровно n вершин, пронумерованных от 1 до n;
- Любая пара вершин i и j, где i ≠ j, соединена ребром тогда и только тогда, когда символы si и sj либо совпадают, либо являются соседними в алфавите. Так, пары букв «a»-«b» и «b»-«c» являются соседними, а пара «a»-«с» — нет.
Вася нарисовал получившийся граф рядом со строкой, а саму строку стёр. На следующий день друг Васи Петя, придя на свою лекцию, обнаружил на своей парте некоторый граф. Он слышал о приключениях Васи и теперь хочет узнать, мог ли это быть тот самый граф G, нарисованный Васей. Для этого Пете требуется знать, существует ли строка s, по которой Вася мог построить такой граф, и если она существует, то хотелось бы получить один из возможных вариантов.
В первой строке входных данных записаны два числа n и m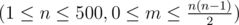 
— количество вершин и рёбер в графе, обнаруженном Петей.
В следующих m строках заданы по два целых числа ui и vi (1 ≤ ui, vi ≤ n, ui ≠ vi), задающие рёбра графа. Гарантируется, что граф не содержит кратных рёбер, то есть любая пара вершин встречается в списке рёбер не более одного раза.
В первой строке выведите «Yes» (без кавычек), если искомая строка существует, и «No» (без кавычек) в противном случае.
Если искомая строка s существует, то выведите её во второй строке. Длина s должна в точности равняться n, все буквы должны быть «a», «b» или «c», а построенный по этой строке граф должен совпадать с заданным во входных данных. Если существует несколько возможных ответов, то разрешается вывести любой.
2 1
1 2
Yes
aa
4 3
1 2
1 3
1 4
No
В первом примере дан граф из двух вершин, между которыми проведено ребро. Значит, эти вершины могут соответствовать как одинаковым буквам, так и соседним. Этому графу удовлетворяет любая из строк «aa», «ab», «ba», «bb», «bc», «cb» и «cc».
Во втором примере первая вершина соединена со всеми остальными тремя вершинами, но эти три вершины не соединены между собой. Это значит, что они должны соответствовать различным буквам, не являющимся соседними, а это невозможно.
