| Codeforces Round 356 (Div. 1) |
|---|
| Закончено |
Лимак — маленький медвежонок, и он плохо отвечает на запросы. Поэтому он просит вас о помощи.
Назовём все неотрицательные целые степени числа 42 (то есть числа 1, 42, 1764, ...) плохими. Все остальные числа являются хорошими.
Вам дана последовательность хороших целых чисел t1, t2, ..., tn. Требуется выполнить q запросов трёх видов:
- 1 i — выведите число ti на отдельной строке.
- 2 a b x — для всех
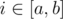 присвоить ti = x. Гарантируется, что число x является хорошим.
присвоить ti = x. Гарантируется, что число x является хорошим. - 3 a b x — для всех
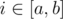 увеличить ti на x. Затем повторять этот процесс до тех пор, пока хотя бы одно число ti является плохим.
увеличить ti на x. Затем повторять этот процесс до тех пор, пока хотя бы одно число ti является плохим.
Несложно заметить, что после выполнения каждого запроса, все числа ti являются хорошими.
В первой строке входных данных записаны два целых числа n и q (1 ≤ n, q ≤ 100 000) — длина последовательности Лимака и количество запросов соответственно.
Во второй строке входных данных записаны n целых чисел t1, t2, ..., tn (2 ≤ ti ≤ 109) — изначальные элементы последовательности Лимака. Гарантируется, что все ti являются хорошими числами.
Далее следуют q строк, описывающих запросы. В i-й из них содержится описание i-го запроса. Первое число каждой из этих строк определяет тип запроса typei (1 ≤ typei ≤ 3). Гарантируется, что во входных данных будет хотя бы один запрос первого типа, то есть корректные выходные данные будут непусты.
Гарантируется, что во всех запросах второго и третьего типов 1 ≤ a ≤ b ≤ n.
Гарантируется, что во всех запросах второго типа целое число x (2 ≤ x ≤ 109) является хорошим. В запросах третьего типа число x (1 ≤ x ≤ 109) может быть плохим.
Для каждого запроса первого типа выведите ответ на отдельной строке.
6 12
40 1700 7 1672 4 1722
3 2 4 42
1 2
1 3
3 2 6 50
1 2
1 4
1 6
2 3 4 41
3 1 5 1
1 1
1 3
1 5
1742
49
1842
1814
1822
43
44
107
После запроса 3 2 4 42 последовательность равна 40, 1742, 49, 1714, 4, 1722.
После запроса 3 2 6 50 последовательность равна 40, 1842, 149, 1814, 104, 1822.
После запроса 2 3 4 41 последовательность равна 40, 1842, 41, 41, 104, 1822.
После запроса 3 1 5 1 последовательность равна 43, 1845, 44, 44, 107, 1822.
| Название |
|---|




