| Codeforces Round 363 (Div. 1) |
|---|
| Закончено |
При создании высоконагруженных систем важную роль играет кэширование данных. В данной задаче пойдёт речь о схеме кэширования LRU (Least Recently Used).
Допустим, размер кэша позволяет хранить не более k объектов. В начале работы программы кэш пуст. При поступлении запроса на обращение к некоторому объекту проверяется его наличие в кэше, и в случае отсутствия объект помещается в кэш. Если после этого в кэше становится больше чем k объектов, то из него удаляется тот объект, который последний раз запрашивался раньше всех, то есть дольше всех не использовался.
Пусть на некотором сервере хранится n видеороликов, причём все видеоролики одинакового размера. Кэш сервера вмещает k видеороликов, и используется схема кэширования, описанная в предыдущем абзаце. Известно, что когда пользователь заходит на сервер и выбирает какой-нибудь ролик для просмотра, вероятность выбрать видеоролик i составляет pi. При этом выбор очередного видеоролика никак не зависит от того, что происходило ранее.
Требуется для каждого видеоролика посчитать вероятность того, что он будет находиться в кэше через 10100 запросов пользователей.
В первой строке входных данных записаны два числа n и k (1 ≤ k ≤ n ≤ 20) — количество видеороликов и размер кэша соответственно. В следующей строке находятся n вещественных чисел pi (0 ≤ pi ≤ 1), заданных с не более чем двумя знаками после запятой.
Гарантируется, что сумма всех pi равняется 1.
Выведите n вещественных чисел, i-е из которых должно равняться вероятности того, что i-й видеоролик будет находиться в кэше через 10100 операций. Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не будет превосходить 10 - 6.
А именно: пусть ваш ответ равен a, а ответ жюри — b. Проверяющая программа будет считать ваш ответ правильным, если 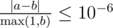 .
.
3 1
0.3 0.2 0.5
0.3 0.2 0.5
2 1
0.0 1.0
0.0 1.0
3 2
0.3 0.2 0.5
0.675 0.4857142857142857 0.8392857142857143
3 3
0.2 0.3 0.5
1.0 1.0 1.0
| Название |
|---|




