| Codeforces Round 364 (Div. 1) |
|---|
| Закончено |
Древляндия — это страна в которой n городов, соединенных n - 1 двусторонней дорогой так, что из любого города можно проехать в любой другой по дорогам.
В Древляндии 2k университетов, расположенных в разных городах.
Недавно Президент подписал указ о соединении университетов высокоскоростной сетью. Министерство образования по своему поняло этот указ, решив что для экономии усилий достаточно каждый университет соединить кабелем с некоторым другим. Формально, указ окажется выполнен!
Для того, чтобы в бюджет заложили максимальную сумму в министерстве решили так разбить университеты на пары, что суммарная длина потраченного кабеля будет максимальна. Иными словами, сумма расстояний между университетами в k парах должна быть как можно больше.
Помогите министерству найти искомую максимальную сумму расстояний. Конечно, каждый университет должен попасть ровно в одну пару. Считайте, что все дороги равны по длине между собой и имеют длины равные 1.
В первой строке входных данных записаны два целых числа n и k (2 ≤ n ≤ 200 000, 1 ≤ k ≤ n / 2) — количество городов в Древляндии и количество пар университетов. Считайте, что города пронумерованы от 1 до n.
Вторая строка содержит 2k различных чисел u1, u2, ..., u2k (1 ≤ ui ≤ n) — номера городов, в которых содержатся университеты.
Следующая n - 1 строка содержит описания дорог. В каждой из этих строк записана пара целых чисел xj, yj (1 ≤ xj, yj ≤ n), которая обозначает, что j-я дорога соединяет города xj и yj. Все дороги двунаправлены. Из любого города можно проехать до любого другого, двигаясь вдоль дорог.
Выведите искомую максимальную сумму расстояний при делении университетов на пары.
7 2
1 5 6 2
1 3
3 2
4 5
3 7
4 3
4 6
6
9 3
3 2 1 6 5 9
8 9
3 2
2 7
3 4
7 6
4 5
2 1
2 8
9
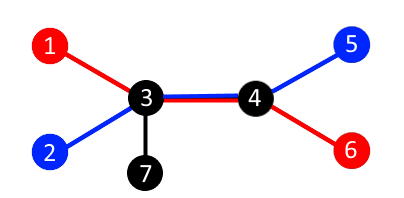
На рисунке ниже представлено одно из возможных оптимальных разбиений на пары для первого тестового примера. Если соединить кабелем университеты номер 1 и 6 (отмечены красным цветом) и университеты номер 2 и 5 (отмечены синим цветом), то суммарное расстояние будет равно 6, что является максимальной суммой для данного примера.
| Название |
|---|




