| AIM Tech Round 3 (Div. 1) |
|---|
| Закончено |
Примерный студент МАИ Алёша получил путёвку в студенческий лагерь Алушта на берегу моря. К сожалению, рядом с лагерем наступила пора сильного бриза, и он рискует быть разрушенным!
Здание лагеря представляет собой прямоугольник высотой n + 2 бетонных блока и шириной m блоков. Каждый день бриз дует с моря, и каждый блок, кроме блоков верхнего и нижнего ряда, левее которого нет других неразрушенных блоков, разрушается с вероятностью  . Аналогично каждую ночь сильный бриз дует на море, и каждый блок, кроме верхнего и нижнего ряда, правее которого нет других неразрушенных блоков, разрушается с той же вероятностью p. Обратите внимание, что верхние и нижние блоки неразрушимы, то есть всего существует n·m разрушимых блоков.
. Аналогично каждую ночь сильный бриз дует на море, и каждый блок, кроме верхнего и нижнего ряда, правее которого нет других неразрушенных блоков, разрушается с той же вероятностью p. Обратите внимание, что верхние и нижние блоки неразрушимы, то есть всего существует n·m разрушимых блоков.
Время бурь продлится k дней и k ночей. В случае если за это время здание лагеря разделится на хотя бы две компоненты связности, оно разрушится, и Алёше придется искать другое времяпрепровождение на лето.
Найдите вероятность того, что Алёше не придётся искать новое занятие на лето, и он сможет отдохнуть в летнем лагере.
В первой строке входных данных заданы два целых числа n и m (1 ≤ n, m ≤ 1500), определяющие размеры разрушимой части здания.
Во второй строке заданы два целых числа a и b (1 ≤ a ≤ b ≤ 109), задающих вероятность разрушения блоков. Гарантируется, что числа a и b взаимно просты.
В третьей строке задано целое число k (0 ≤ k ≤ 100 000) — количество дней и ночей, в течение которых будет дуть сильный ветер.
Пусть ответ в виде несократимой дроби равен  . Выведите одно целое число, равное
. Выведите одно целое число, равное 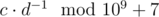 . Гарантируется, что при данных ограничениях
. Гарантируется, что при данных ограничениях 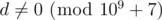 .
.
2 2
1 2
1
937500007
5 1
3 10
1
95964640
3 3
1 10
5
927188454
В первом тестовом примере каждый из четырёх блоков разрушается с вероятностью  . Для того чтобы здание не разрушилось, существует 7 вариантов того, как может выглядеть здание после одного дня, если оно не потеряло связность, то есть искомая вероятность равна
. Для того чтобы здание не разрушилось, существует 7 вариантов того, как может выглядеть здание после одного дня, если оно не потеряло связность, то есть искомая вероятность равна 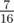 , а значит нужно вывести
, а значит нужно вывести 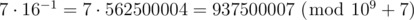

| Название |
|---|




