| Codeforces Round 369 (Div. 2) |
|---|
| Закончено |
Кодер ZS и Бабуин Крис довольно долго путешествовали по Удайлэнду. Они узнали, что он состоит из n городов, пронумерованных от 1 до n.
В Удайлэнде существует ровно n направленных дорог. i-ая из них выходит из города с номером i и ведет в другой город с номером ai (ai ≠ i). Кодер ZS может поменять направление любой из дорог в Удайлэнде, то есть, если дорога вела от города A к городу B до смены направления, она будет вести от города B к городу A после него.
Кодер ZS считает дороги в Удайлэнде запутанными, если существует последовательность различных городов A1, A2, ..., Ak (k > 1), таких, что для каждого 1 ≤ i < k существует дорога, ведущая из города Ai в город Ai + 1 и еще одна из города Ak в город A1. Другими словами, дороги запутанные, если некоторые из них образуют направленный цикл из каких-то городов.
Теперь Кодеру ZS'у интересно, сколько наборов дорог изначальной конфигурации (всего их 2n) он может выбрать, таких, что после смены направления каждой из дорог в наборе ровно по одному разу, результирующая сеть дорог не будет запутанной.
Заметьте, что после смены направления позволяется существовать городу, из которого выходит несколько дорог, или городу, из которого не выходит ни одной дороги, или нескольким дорогам между одной и той же парой городов.
Первая строка содержит единственное целое число n (2 ≤ n ≤ 2·105) — количество городов в Удайлэнде.
Следующая строка содержит n целых чисел a1, a2, ..., an (1 ≤ ai ≤ n, ai ≠ i), ai означает, что существует дорога, ведущая из города i в город ai.
Выведите единственное целое число — количество способов поменять направление какого-нибудь набора дорог так, что весь набор дорог станет не запутанным. Так как ответ может быть очень большим, выведите остаток от его деления на 109 + 7.
3
2 3 1
6
4
2 1 1 1
8
5
2 4 2 5 3
28
Рассмотрим первый пример из условия. Существует 3 города и 3 дороги. Города пронумерованы от 1 до 3, а дороги изначально имеют вид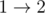 
, 
, 
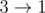. Пронумеруем дороги от 1 до 3 в соответствующем порядке.
Наборы дорог, для которых Кодер ZS может сменить направление (чтобы сделать дороги не запутанными), это наборы {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}. Заметьте, что пустой набор дорог не подходит, поскольку, если не менять направление ни одной дороги, то города 1, 2, 3 образуют направленный цикл, так что дороги будут запутанными. Аналогично, смена направления каждой дороги приводит к запутанной конфигурации. Таким образом, всего существует 6 возможных наборов, для которых Кодер ZS может поменять направление.
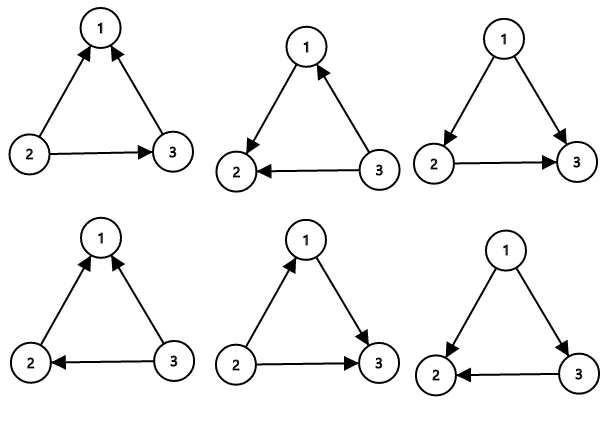
Следующий рисунок изображает всевозможные способы ориентации дорог из первого примера так, что сеть дорог не является запутанной:
