| VK Cup 2017 - Раунд 1 |
|---|
| Закончено |
Мишка Лимак исследует социальную сеть. Основная ее функциональность заключается в том, что два пользователя могут стать друзьями (в таком случае они могут обмениваться сообщениями и смешными картинками).
Сейчас в социальной сети n пользователей, они пронумерованы от 1 до n. Ровно m пар из них являются друзьями. Конечно. никакой пользователь не может быть другом с самим собой.
Пусть запись A-B означает, что пользователи A and B друзья. Лимак считает, что социальная сеть обоснована, если и только если выполняется следующее условие: для любых трех различных пользователей (X, Y, Z) если X-Y и Y-Z, то также X-Z.
Например, если Алан и Боб друзья, и Боб и Цири друзья, то Алан и Цири тоже должны быть друзьями.
Можете помочь Лимаку и проверить, что социальная сеть обоснована? Выведите «YES» или «NO» без кавычек в соответствии с результатом.
Первая строка содержит два целых числа n и m (3 ≤ n ≤ 150 000,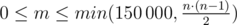 
) — число пользователей сети и число пар пользователей, которые являются друзьями.
i-я из следующих m строк содержит два целых различных числа ai и bi (1 ≤ ai, bi ≤ n, ai ≠ bi), означающих, что ai-й и bi-й пользователи являются друзьями. Все пары друзей различны.
Если данная социальная сеть обоснована, выведите в единственную строку «YES» (без кавычек).
Иначе выведите в единственную строку «NO» (без кавычек).
4 3
1 3
3 4
1 4
YES
4 4
3 1
2 3
3 4
1 2
NO
10 4
4 3
5 10
8 9
1 2
YES
3 2
1 2
2 3
NO
Рисунки ниже показывают социальную сеть в первом (слева) и во втором (справа) примерах. Кружки обозначают пользователей, а линии означают, что два пользователя являются друзьями.
Во втором примере ответ «NO», потому что пользователи (2, 3) друзья, пользователи (3, 4) тоже друзья, а пользователи (2, 4) — нет.
