| VK Cup 2017 - Раунд 1 |
|---|
| Закончено |
Деревом называется неориентированный ациклический связный граф. Расстоянием между двумя вершинами называется число ребер на простом пути между ними.
Лимак — маленький полярный мишка. Он живет на дереве, состоящем из n вершин, вершины дерева пронумерованы от 1 до n.
Недавно Лимак научился прыгать. Он может прыгнуть из некоторой вершины в любую вершину на расстоянии не дальше k.
Для пары вершин (s, t) определим f(s, t) как минимальное число прыжков, которое требуется Лимаку, чтобы попасть из вершины s в вершину t. Найдите сумму величин f(s, t) по всем парам вершин (s, t) таким, что s < t.
В первой строке содержатся два целых числа n и k (2 ≤ n ≤ 200 000, 1 ≤ k ≤ 5) — число вершин в дереве и максимальное расстояние, на которое может прыгнуть Лимак, соответственно.
Следующие n - 1 строк содержат описания ребер дерева. i-я из этих строк содержит два целых числа ai и bi (1 ≤ ai, bi ≤ n) — номера вершин, соединенных i-м ребром.
Гарантируется, что заданный граф является деревом.
Выведите одно число — сумму величин f(s, t) по всем парам вершин (s, t) таким, что s < t.
6 2
1 2
1 3
2 4
2 5
4 6
20
13 3
1 2
3 2
4 2
5 2
3 6
10 6
6 7
6 13
5 8
5 9
9 11
11 12
114
3 5
2 1
3 1
3
В первом примере дерево состоит из 6 вершин и показано на рисунке ниже. Лимак может прыгать в любую вершину на расстоянии не больше 2 от текущей. Например, из вершины 5 он может прыгнуть в вершины 1, 2 и 4 (а также в саму вершину 5).
Всего есть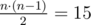 
пар вершин (s, t) таких, что s < t. Для 5 из этих пар Лимаку понадобится два прыжка, это пары (1, 6), (3, 4), (3, 5), (3, 6), (5, 6). Для остальных 10 пар вершин достаточно одного прыжка. Таким образом, ответ равен 5·2 + 10·1 = 20.
В третьем примере Limak может прыгать из любой вершины в любую. Всего есть 3 пары вершин (s < t), поэтому ответ равен 3·1 = 3.
