| VK Cup 2017 - Раунд 1 |
|---|
| Закончено |
У Лимака есть таблица из 2 строк и n столбцов. Ячейка j строки i содержит целое число ti, j, которое может быть положительным, отрицательным или нулем.
Непустой прямоугольник из ячеек назовем красивым, если и только если сумма чисел в его ячейках равна 0.
Лимак хочет выбрать несколько красивых прямоугольников и подарить их друзьям. Никакие два выбранных прямоугольника не могут иметь общих ячеек. Какое максимальное число красивых прямоугольников может выбрать Лимак?
В первой строке находится единственное целое число n (1 ≤ n ≤ 300 000) — количество столбцов в таблице.
Следующие две строки содержат числа, записанные в ячейках. i-я из этих строк содержит n целых чисел ti, 1, ti, 2, ..., ti, n ( - 109 ≤ ti, j ≤ 109).
Выведите одно целое число — максимальное число непересекающихся по ячейкам красивых прямоугольников.
6
70 70 70 70 70 -15
90 -60 -30 30 -30 15
3
4
0 -1 0 0
0 0 1 0
6
3
1000000000 999999999 -1000000000
999999999 -1000000000 -999999998
1
В первом примере всего четыре красивых прямоугольника:
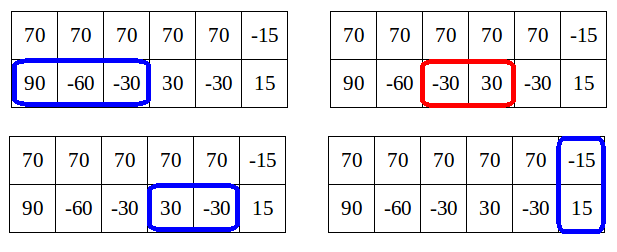
Лимак не может выбрать все их них, потому что они пересекаются. Он может выбрать максимум три прямоугольника: те, которые обведены синим на рисунке.
Во втором примере оптимально выбрать шесть красивых прямоугольников, каждый из них состоит из одной ячейки с числом 0.
В третьем примере единственный красивый прямоугольник — это вся таблица. Сумма всех чисел равна 0. Очевидно, Лимак может взять не больше одного красивого прямоугольника, поэтому ответ 1.
| Название |
|---|




