| VK Cup 2017 - Раунд 2 |
|---|
| Закончено |
У вас есть выпуклый многоугольник P, вершины которого расположены в n различных точках p1, p2, ..., pn. Точка pi имеет координаты (xi, yi) на плоскости. Точки перечислены в порядке обхода по часовой стрелке.
Вы можете выбрать вещественное число D и передвинуть каждую из вершин многоугольника из начального положения в любую точку на расстоянии не больше D.
Найдите максимальное значение D такое, что независимо от того, как вы передвинете вершины, многоугольник не пересечет сам себя и останется выпуклым.
Первая строка содержит одно целое число n (4 ≤ n ≤ 1 000) — количество вершин в многоугольнике.
Следующие n строк содержат координаты вершин многоугольника. Строка i содержит два целых числа xi и yi ( - 109 ≤ xi, yi ≤ 109) — изначальные координаты вершины i. Гарантируется, что точки даны в порядке обхода по часовой стрелке, и они образуют строго выпуклый многоугольник (в частности, никакие три последовательные точки не лежат на одной прямой).
Выведите одно вещественное число — максимальное из таких D, что независимо от того, как вы передвинете вершины, многоугольник не пересечет сам себя и останется выпуклым.
Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не превосходит 10 - 6.
А именно, пусть ваш ответ равен a, а ответ жюри равен b. Ваш ответ будет засчитан, если 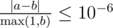 .
.
4
0 0
0 1
1 1
1 0
0.3535533906
6
5 0
10 0
12 -4
10 -8
5 -8
3 -4
1.0000000000
Иллюстрация к первому примеру:

Вот пример того, как можно сделать многоугольник невыпуклым:

Это — не оптимальный ответ, так как максимальное расстояние, на которое мы сдвинули вершину, около ≈ 0.4242640687, в то время как можно сделать многоугольник невыпуклым, сдвинув каждую точку на расстояние не более ≈ 0.3535533906.
| Название |
|---|




