| VK Cup 2017 - Раунд 3 |
|---|
| Закончено |
В стране Невер n городов и очень хорошо развитая дорожная сеть. Между каждой парой городов есть ровно одна двусторонняя дорога, таким образом, всего в Невере целых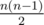 
дорог! При этом никакая дорога не пересекается ни с какой другой дорогой и не проходит через промежуточные города. Что-что, а туннели и мосты в Невере строить умели.
Независимая комиссия оценила каждую дорогу Невера положительным целым числом, называемым тленностью дороги. Чем ниже тленность, тем приятнее по дороге ехать.
В рамках года транспорта в Невере было решено построить музей транспорта в одном из городов страны, а в каждом другом городе установить ровно один указатель на некоторый город (не обязательно тот, в котором находится музей). Указатели должны удовлетворять следующему важному требованию: если любой неверец, живущий в городе без музея, отправится из своего родного города по указателям, то рано или поздно обязательно приедет в город с музеем.
Неверцы — невероятно положительно настроенные люди. Если неверец отправился по маршруту, состоящему из нескольких дорог, то тленностью маршрута неверец считает минимальную из тленностей дорог в этом маршруте.
Руководство Невера еще не приняло окончательное решение относительно города, в котором следует построить музей, и рассматривает все n возможных вариантов. Принципиальное значение имеет сумма тленностей маршрутов до города с музеем из всех остальных городов страны, если путники будут строго следовать установленным указателям. Руководство Невера заботится о своих жителях, поэтому они хотели бы направить указатели таким образом, чтобы минимизировать эту сумму. Помогите им определить минимальное возможное её значение при всех n вариантах строительства музея.
В первой строке содержится число n (2 ≤ n ≤ 2000) — количество городов в Невере.
Следующие n - 1 строк содержат описание дорожной сети. i-я из этих строк содержит n - i целых чисел. j-е число в i-й строке обозначает тленность дороги между городами i и i + j.
Все тленности дорог находятся в диапазоне от 1 до 109, включительно.
Для каждого города в порядке от 1 до n выведите минимальную возможную сумму тленностей маршрутов до данного города из всех остальных городов при оптимальной установке указателей.
3
1 2
3
2
2
3
6
2 9 9 6 6
7 1 9 10
9 2 5
4 10
8
6
5
7
5
7
11
Первый пример пояснен рисунком ниже. Слева направо изображены исходная дорожная сеть и оптимальные расстановки указателей при строительстве музея в городах 1, 2 и 3, соответственно. Синим цветом обозначен город с музеем, зеленым — направление указателя в каждом другом городе.
Например, при строительстве музея в городе 3 следует направить указатель в городе 1 на город 3, а указатель в городе 2 — на город 1. Тогда маршрут из города 1 до города 3 будет иметь тленность 2, а маршрут из города 2 до города 3 — тленность 1. Сумма тленностей данных маршрутов составит 3.
