Недавно Андрюша нашел удивительный игровой автомат. Он представлял из себя доску, расположенную вертикально, разбитую на квадраты. Всего на доске было w столбцов, пронумерованных от 1 до w слева направо, и h строк, пронумерованных снизу вверх от 1 до h.
Кроме того, в некоторых строках автомата были расположены перегородки. Всего перегородок было n, и i-я из них располагалась в строке ui, занимая все клетки в столбцах с li по ri. Никакие две перегородки не находились в одной строке, Андрюша это точно запомнил. Кроме того, в каждой строке была хотя бы одна клетка, в которой не было перегородки.
В любой столбец автомата можно было сверху бросить шарик. В таком случае шарик начинал падать вниз, пока не натыкался на какую-либо перегородку или не выпадал из автомата снизу. Если шарик натыкался на перегородку, то он исчезал, а вместо него возникали два шарика слева и справа от перегородки, и продолжали падать по тем же правилам. Если слева или справа от перегородки находился край доски, то оба шарика появлялись с той стороны, где нет края. При этом могло быть, что в какой-то клетке оказывались два или более шарика одновременно, это никак не влияло на их движение. В конце все шарики выпадали из автомата снизу.
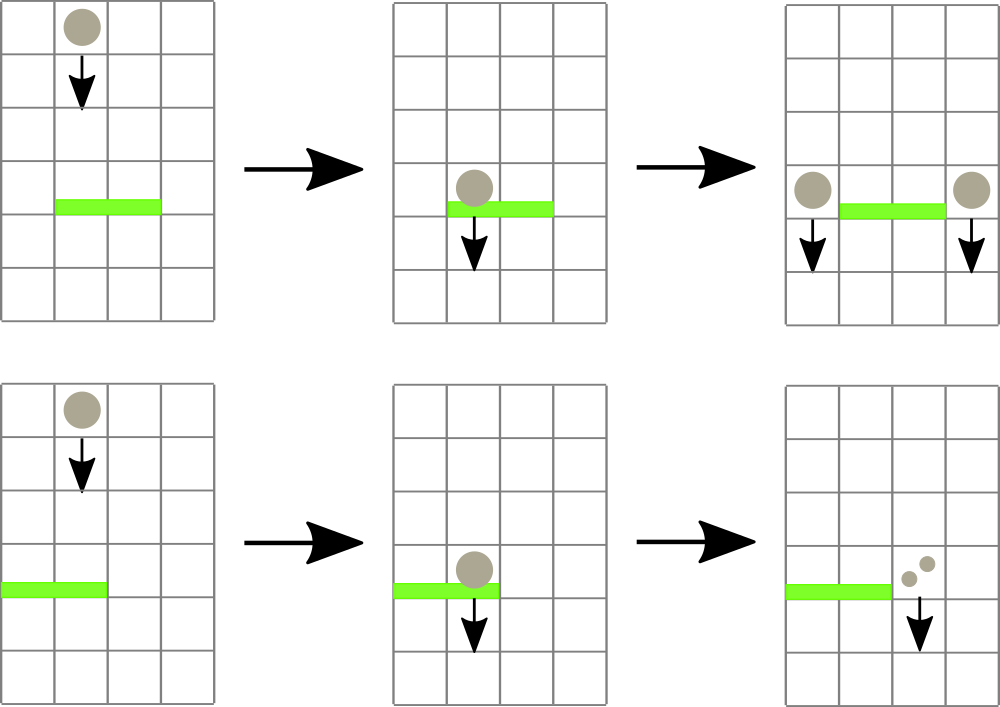Примеры того, как шарики взаимодействуют с барьерами. Особенность автомата была в том, что иногда шарики проходили сквозь перегородки, как через свободные клетки. Это связано с тем, что перегородки были живыми и боялись шариков, падающих с большой высоты. А именно, если на перегородку номер i падал шарик, который перед этим падал более, чем si клеток (то есть шарик появился в строке с номером строго больше, чем ui + si), то перегородка пропускает этот шарик, как будто ее нет. Если шарик был брошен в автомат сверху, считайте, что он появился на высоте (h + 1).
Андрюша помнит, что он бросил по одному шарику в каждый из столбцов. Найдите для него общее количество шариков, выпавших снизу. Так как это число может быть большим, выведите остаток от деления этого числа на 109 + 7.
В первой строке находятся три целых числа h, w и n (1 ≤ h ≤ 109, 2 ≤ w ≤ 105, 0 ≤ n ≤ 105) — число строк, число столбцов и число перегородок в автомате.
В каждая из следующих n строк находятся четыре целых числа. В i-й из этих строк находятся числа ui, li, ri, si (1 ≤ ui ≤ h, 1 ≤ li ≤ ri ≤ w, 1 ≤ si ≤ 109) — строка, в которой находится i-я перегородка. столбцы, в которых находятся края этой перегородки, и максимальная высота, с которой перегородка не пропускает шарики. Гарантируется, что в каждой строке есть хотя бы одна клетка, в которой нет перегородки, а также то, что все ui различны.
Выведите единственное число — остаток от деления суммарного числа выпавших шариков на 109 + 7.
10 5 1
3 2 3 10
7
10 5 2
3 1 3 10
5 3 5 10
16
10 5 2
3 1 3 7
5 3 5 10
14
10 15 4
7 3 9 5
6 4 10 1
1 1 4 10
4 11 11 20
53
В первом примере один барьер: если бросить шарик во второй или третий столбец, то выпадет два шарика, иначе — один. Итого ответ 7.
Во втором примере количество выпавших шариков равно 2, 2, 4, 4, 4 при бросании шариков в столбцы слева направо соответственно.
В третьем примере количество выпавших шариков равно 1, 1, 4, 4, 4 при бросании шариков в столбцы слева направо соответственно. Обратите внимание, первый барьер пропускает шарики, падающие на него напрямую, но не пропускает те, что падают на него со второго барьера.
В четвертом примере количество выпавших шариков равно 2, 2, 6, 6, 6, 6, 6, 6, 6, 1, 2, 1, 1, 1, 1 при бросании шариков в столбцы слева направо соответственно. Случай, когда шарик брошен в седьмой столбец, рассмотрен на рисунке ниже.
Результат, если бросить шарик в седьмой столбец.
