| Educational Codeforces Round 18 |
|---|
| Закончено |
Пусть T — полное бинарное дерево, состоящее из n вершин. Это означает, что ровно одна вершина является его корнем и у каждой вершины либо ровно два сына (левый и правый), либо нет сыновей (вершина является листом). Все листы полного бинарного дерева находятся на одинаковом расстоянии от корня. Очевидно, число n таково, что n + 1 обязательно является степенью числа 2.
На рисунке ниже изображен пример полного бинарного дерева для n = 15.
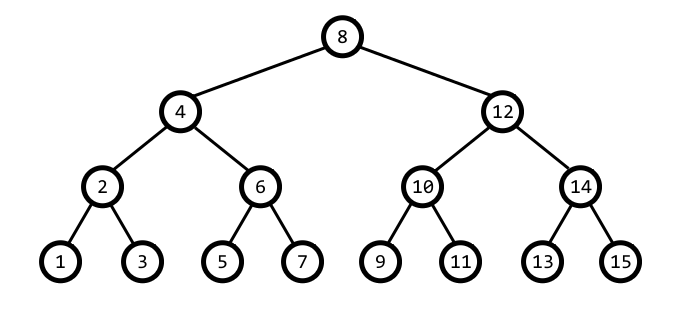
Вершины дерева будем нумеровать от 1 до n специальным образом. Нумерацию будем производить рекурсивным образом: сначала рекурсивно назначим номера вершинам левого поддерева (если оно есть), затем дадим очередной номер текущей вершине, а после этого рекурсивно назначим номера вершинам правого поддерева (если оно есть). Номера на рисунке выше назначены именно таким образом. Отметим, что описанный способ однозначно определяет номера вершин. Такой порядок обхода бинарного дерева называется симметричным.
Напишите программу, которая по заданному числу n и q запросам возвращает ответ на каждый из них.
Каждый из запросов — это целое число ui (1 ≤ ui ≤ n) и строка si, где ui — номер вершины, а si — описание пути из этой вершины. Строка si содержит исключительно буквы 'L', 'R' и 'U', которые обозначают переход к левому сыну, переход к правому сыну и переход к родительской вершине соответственно. Символы в строке si следует обрабатывать последовательно слева направо, считая стартовой вершину ui. Если переход невозможен, то его следует проигнорировать. Ответом на запрос является номер вершины, в которой будет завершен путь si.
Например, если ui = 4 и si = «UURL», то ответом будет вершина 10.
В первой строке входных данных содержатся два целых числа n и q (1 ≤ n ≤ 1018, q ≥ 1). Значение n таково, что n + 1 является степенью числа 2.
Следующие 2q строк содержат описания запросов парами строк. Первая из них содержит целое число ui (1 ≤ ui ≤ n), вторая — непустую строку si. Строка si содержит исключительно буквы 'L', 'R' и 'U'.
Гарантируется, что сумма длин строк si для всех i (1 ≤ i ≤ q) не превосходит 105.
Выведите q чисел, i-е из них должно быть равно ответу на i-й запрос.
15 2
4
UURL
8
LRLLLLLLLL
10
5
| Название |
|---|




