| Educational Codeforces Round 22 |
|---|
| Закончено |
Алисе надоели обычные правила игры в догонялки, и она предложила Бобу немного их изменить. Теперь игра происходит на неориентированном корневом дереве из n вершин. Вершина 1 является корнем дерева.
Алиса начинает в вершине 1, а Боб — в вершине x (x ≠ 1). Ходы совершаются по очереди, Боб начинает. За один ход игрок может либо остаться в текущей вершине, либо перейти в соседнюю.
Игра завершается, когда Алиса приходит в вершину, в которой находится Боб. Алиса хочет минимизировать общее количество ходов, Боб хочет максимизировать.
Напишите программу, которая определит, сколько ходов продлится игра.
В первой строке записано два целых числа n и x (2 ≤ n ≤ 2·105, 2 ≤ x ≤ n).
В каждой из следующих n - 1 строк записано по два целых числа a и b (1 ≤ a, b ≤ n) — ребра дерева. Гарантируется, что ребра составляют корректное дерево.
Выведите общее количество ходов, которые будут совершены Алисой и Бобом.
4 3
1 2
2 3
2 4
4
5 2
1 2
2 3
3 4
2 5
6
В первом примере дерево выглядит так:
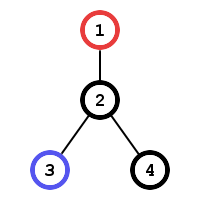
Красная вершина — начальная позиция Алисы, синяя — Боба. Боб обеспечит самую долгую игру, если будет оставаться в вершине 3.
B: стоит в вершине 3
A: идет в вершину 2
B: стоит в вершине 3
A: идет в вершину 3
Во втором примере дерево выглядит так:
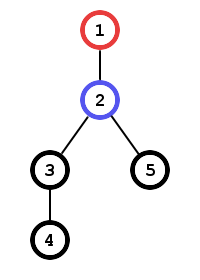
Ходы в оптимальной стратегии:
B: идет в вершину 3
A: идет в вершину 2
B: идет в вершину 4
A: идет в вершину 3
B: стоит в вершине 4
A: идет в вершину 4
| Название |
|---|




