| Codeforces Round 418 (Div. 2) |
|---|
| Закончено |
Те, кто не хотят возвращаться домой из дальнего путешествия, будут поражены болезнью улитки и потеряются. Майои, переносчик болезни, не хочет, чтобы такое случалось, но не может ничем помочь до того, как найдется лекарство. Сейчас она лишь хочет узнать, насколько сложно придется потерявшемуся.
В регионе находятся n городов, пронумерованных от 1 до n, город номер 1 является столицей. Сеть дорог образована двусторонними дорогами равной длины, каждая из которых соединяет два города. Никакие две дороги не соединяют одинаковые пары городов, и никакая дорога не соединяет город сам с собой. Потерявшиеся не могут узнать, как устроена сеть, но жители могут предоставить следующую информацию:
- Из любого города существует ровно один кратчайший (по числу дорог) путь до столицы;
- Пусть расстояние от города i до столицы равно li. Тогда li ≥ li - 1 выполняется для всех 2 ≤ i ≤ n;
- К городу i подходит ровно di дорог, и это число равно либо 2, либо 3.
Подсчитайте, сколько различных сетей дорог существует с заданными ограничениями и выведите ответ по модулю 109 + 7. Две сети считаются различными, если есть пара (u, v) (1 ≤ u, v ≤ n) такая, что в одной сети есть дорога между городами u и v, а в другой такой дороги нет.
В первой строке находится целое число n (3 ≤ n ≤ 50) — количество городов.
Во второй строке находятся n целых чисел d1, d2, ..., dn (2 ≤ di ≤ 3) — количество дорог, подходящих к городам 1, 2, ..., n, соответственно. Гарантируется, что сумма di по всем i четна.
Выведите одно число — число различных графов по модулю 109 + 7.
4
3 2 3 2
1
5
2 3 3 2 2
2
5
2 2 2 2 2
2
20
2 2 2 2 3 2 3 2 2 2 2 2 2 2 2 2 2 3 3 2
82944
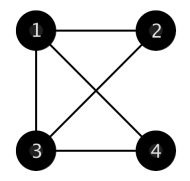
В первом примере следующая сеть — единственная, удовлетворяющая ограничениям. Все расстояния из столицы до городов 2, 3, 4 равны 1.
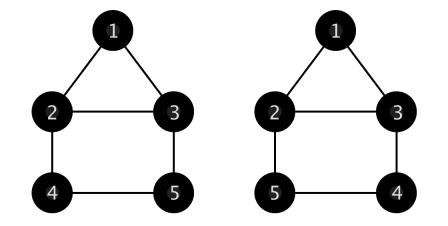
Во втором примере следующие две сети удовлетворяют условию:
| Название |
|---|




