| Codeforces Round 420 (Div. 2) |
|---|
| Закончено |
Окабэ любит гулять по городу в освещенных лампами местах. Так ему удается избежать нападения школьников.
Город Окабэ представлен как таблица, строки пронумерованы от 1 до n сверху вниз, столбцы пронумерованы от 1 до m слева направо. Ровно k клеток города освещены лампами. Гарантируется, что левая верхняя клетка освещена.
Окабэ начинает свой путь из верхней левой клетки и хочет попасть в правую нижнюю. Конечно, Окабэ будет ходить только по освещенным клеткам, и может перемещаться из клетки только в соседнюю сверху, снизу, слева или справа. Однако, Окабэ может временно подсветить все клетки в одном столбце или строке, если он заплатит 1 монету, что позволит ему проходить по некоторым клеткам, не подсвеченным изначально.
Заметьте, что Окабэ может подсветить только один столбец или одну строку одновременно, и должен заплатить монету каждый раз, когда подсвечивает новый столбец или строку. Чтобы изменить строку или столбец, подсвеченный временно, он должен стоять в клетке, которая подсвечена изначально. Кроме того, как только он убирает временную подсветку со строки или столбца, все клетки этой строки/столбца, не подсвеченные изначально, перестают быть освещены.
Помогите Окабэ найти минимальное число монет, которое он должен заплатить, чтобы достичь своей цели!
Первая строка содержит три целых числа n, m и k (2 ≤ n, m, k ≤ 104).
Каждая из следующих k строк содержит два целых числа ri и ci (1 ≤ ri ≤ n, 1 ≤ ci ≤ m) — строку и столбец, в которых находится i-я подсвеченная клетка.
Гарантируются, что все k подсвеченных клеток различны. Гарантируется, что верхняя левая клетка подсвечена.
Выведите минимальное число монет, которое должен заплатить Окабэ, чтобы достичь правой нижней клетки, или -1, если это невозможно.
4 4 5
1 1
2 1
2 3
3 3
4 3
2
5 5 4
1 1
2 1
3 1
3 2
-1
2 2 4
1 1
1 2
2 1
2 2
0
5 5 4
1 1
2 2
3 3
4 4
3
В первом примере Окабэ может пройти по пути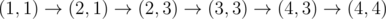 
, заплатив только перед перемещениями в (2, 3) и (4, 4).
В четвертом примере Окабэ может пройти по пути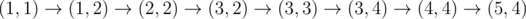 
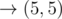, заплатив перед переходами в (1, 2), (3, 4) и (5, 4).
