| Educational Codeforces Round 25 |
|---|
| Закончено |
Макес решает задачи на Decoforces и множестве других онлайн платформ. Каждая задача характеризуется своей сложностью — целым положительным числом. Сложности измеряются одинаково на всех платформах (т.е. задача со сложностью d на Decoforces такая же трудная, как и задача со сложностью d на любой другой платформе).
Макес выбрал для решения n задач на Decoforces со сложностями a1, a2, ..., an. Он может решать задачи в произвольном порядке. Однако, чтобы решить задачу i со сложностью ai, надо заранее решить хотя бы одну задачу со сложностью 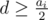 (не имеет значения, на какой платформе).
(не имеет значения, на какой платформе).
Перед решением выбранного списка задач Макес уже решал задачи с максимальной сложностью k.
С заданными условиями легко заметить, что Макес не всегда может решить все выбранные задачи, какой бы порядок он не использовал. Поэтому он хочет решить некоторые задачи на других платформах так, чтобы завершить решение задач из своего списка.
Для каждого целого положительного y хотя бы на одной платформе помимо Decoforces существует задача со сложностью y.
Макес может решать задачи на любой платформе в любое время, не обязательно решать задачи из списка подряд одну за другой.
У Макеса не очень много свободного времени, поэтому он просит вас посчитать минимальное количество задач, которые ему потребуется решить на других платформах, чтобы решить все выбранные задачи на Decoforces.
В первой строке записаны два целых числа n, k (1 ≤ n ≤ 103, 1 ≤ k ≤ 109).
Во второй строке записаны n целых чисел, разделенных пробелами, a1, a2, ..., an (1 ≤ ai ≤ 109).
Выведите минимальное количество задач, которые Макесу потребуется решить на других платформах, чтобы решить все выбранные задачи на Decoforces.
3 3
2 1 9
1
4 20
10 3 6 3
0
В первом примере Макес сначала решает задачи 1 и 2. Потом, чтобы решить задачу со сложностью 9, он должен сначала решить задачу со сложностью не меньше 5. Единственные доступные — сложности 5 и 6 на каких-то других платформах. Решение одной из этих задач даст Макесу возможность решить задачу 3.
Во втором примере он может решить каждую задачу с самого начала.
| Название |
|---|




