| Яндекс.Алгоритм 2011: Раунд 2 |
|---|
| Закончено |
В редких перерывах между поисками теории всего физик Воль играет в расслабляющую игру — модифицированный им тетрис.
Компьютер выдает Волю прямоугольное игровое поле n × m, на котором некоторые клетки пустые, остальные же заполнены. Игровая панель рядом с полем содержит изображения всевозможных связных фигурок, содержащих от двух до пяти клеток. Здесь мы рассматриваем только связные по стороне фигурки. Фигурки можно копировать с игровой панели на поле, заполняя ими пустые клетки. Разумеется, каждую фигурку можно использовать сколько угодно раз.
Задача Воля — заполнить все поле так, чтобы на нем не осталось пустых клеток.
Каждая изначально свободная клетка должна оказаться покрыта ровно одной клеткой некоторой фигурки. Каждая фигурка должна полностью находиться на игровом поле.
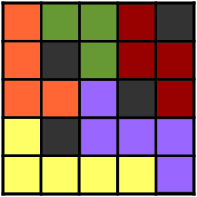
На рисунке черные клетки — изначально заполненные клетки поля, а одноцветные связные области — фигурки.
Первая строка содержит целые числа n и m (1 ≤ n, m ≤ 1000), n и m — высота и ширина поля соответственно. Следующие n строк содержат по m символов каждая. Они естественным образом описывают поле: j-ый символ i-ой строки равен «#», если соответствующая клетка поля занята, и «.», если соответствующая клетка поля свободна и должна быть покрыта некоторой фигуркой.
Если поле заполнить невозможно, выведите единственной число «-1» (без кавычек). Иначе выведите любое заполнение поля фигурками в формате, совпадающем с входным, где все «.» (пустые клетки) заменены описанием фигурок следующим образом (см. примеры): каждая фигурка должна быть выведена конкретной цифрой, при этом касающимся по стороне фигуркам должны соответствовать разные цифры.
2 3
...
#.#
000
#0#
3 3
.#.
...
..#
5#1
511
55#
3 3
...
.##
.#.
-1
1 2
##
##
В третьем примере невозможно заполнить пустую клетку, у которой нет пустых соседей.
В четвертом примере ничего заполнять не нужно, поэтому надо вывести исходное поле.
| Название |
|---|




