| Hello 2018 |
|---|
| Закончено |
Рассмотрим корневое дерево. В корневом дереве есть одна выделенная вершина — корень. Все ребра ориентированы по направлению от корня. Вершина u является ребенком вершины v, а вершина v является родителем вершины u, если существует ориентированное ребро из v в u. Листом корневого дерева называется вершина, у которой нет детей, и есть родитель.
Назовем корневое дерево елкой, если у каждой вершины, не являющейся листом, хотя бы 3 ребенка являются листами. Вам дано корневое дерево, проверьте, является ли оно елкой.
Определение корневого дерева можно прочитать по ссылке.
В первой строке дано одно целое число n — количество вершин в дереве (3 ≤ n ≤ 1 000). В следующих n - 1 строках даны целые числа pi (1 ≤ i ≤ n - 1) — номер вершины, являющейся родителем i + 1-й вершины (1 ≤ pi ≤ i).
Вершина с номером 1 является корнем дерева. Гарантируется, что у корня как минимум 2 ребенка.
Выведите «Yes», если дерево является елкой, и «No» иначе.
4
1
1
1
Yes
7
1
1
1
2
2
2
No
8
1
1
1
1
3
3
3
Yes
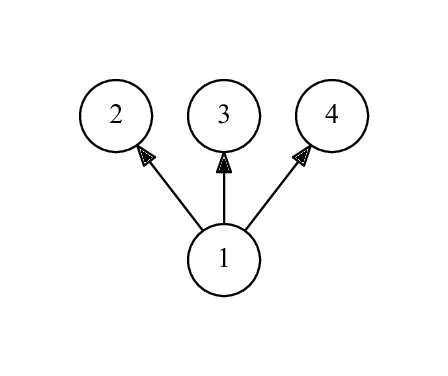
Первый пример:
Второй пример:
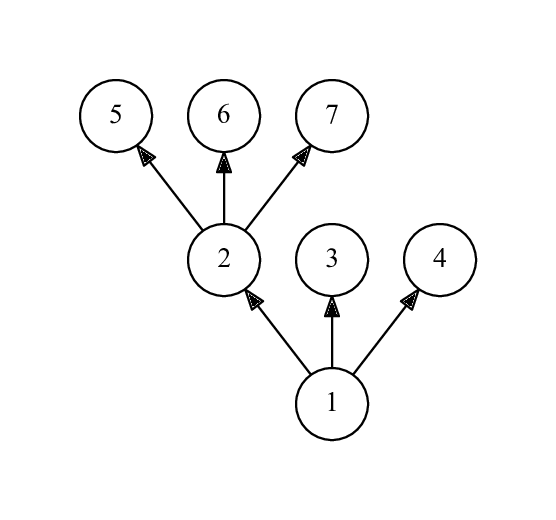
Это не елка, потому что у вершины 1, которая не является листом, только 2 ребенка являются листьями.
Третий пример:
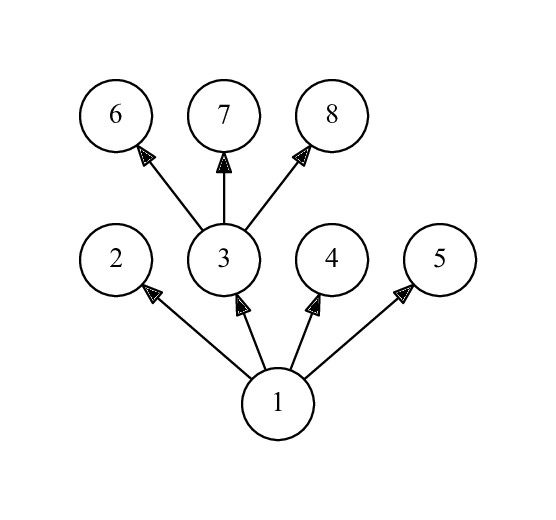
| Название |
|---|




