| Hello 2018 |
|---|
| Закончено |
Вам дана булева функция от трех переменных, заданная своей таблицей истинности. Требуется построить минимальное по длине выражение, равное этой функции. Выражение может содержать:
- Операцию И ('&', ASCII код 38)
- Операцию ИЛИ ('|', ASCII код 124)
- Операцию НЕ ('!', ASCII код 33)
- Переменные x, y и z (ASCII коды 120-122)
- Круглые скобки ('(', ASCII код 40, и ')', ASCII код 41)
Если выражений несколько, требуется найти лексикографически минимальное.
Операции имеют стандартный приоритет: самый большой приоритет у НЕ, затем идет И, а самый маленький приоритет у ИЛИ. Формально, выражение должно удовлетворять следующей грамматике:
E ::= E '|' T | T
T ::= T '&' F | F
F ::= '!' F | '(' E ')' | 'x' | 'y' | 'z'
В первой строке дано одно целое число n — количество функций, для которых нужно найти ответ (1 ≤ n ≤ 10 000).
В следующих n строках дано описание функций, в i-й строке дана строка длины 8, состоящая из символов 0 и 1 — таблица истинности i-й функции. Символ на позиции j (0 ≤ j < 8) означает, что должна возвращать функция, если ей на вход подать 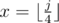 ,
, 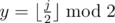 и
и 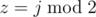 .
.
Выведите n строк, в i-й должно содержаться выражение минимальной длины, равное i-й функции. Если выражений минимальной длины несколько, нужно вывести лексикографически минимальное. Выражения должны удовлетворять грамматике из условия и не должны содержать пробельных символов.
4
00110011
00000111
11110000
00011111
y
(y|z)&x
!x
x|y&z
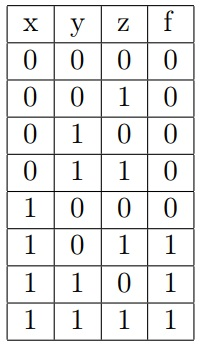
Таблица истинности для второй функции:
| Название |
|---|




