| Codeforces Round 457 (Div. 2) |
|---|
| Закончено |
Джейми называет неориентированный взвешенный граф интересным если он обладает следующими свойствами:
- Граф связен и содержит ровно n вершин и m рёбер.
- Все веса рёбер — целые числа и принадлежат отрезку [1, 109].
- Вес кратчайшего пути из вершины 1 в n является простым числом.
- Сумма весов рёбер в минимальном остовном дереве графа является простым числом.
- Граф не содержит петель и кратных рёбер.
В разделе «Примечание» содержатся описания терминов выше.
Помогите Джейми найти какой-нибудь интересный граф.
В первой строке содержатся два целых числа n и m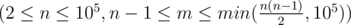 
— требуемое количество вершин и рёбер.
В первой строке выведите два целых числа sp, mstw (1 ≤ sp, mstw ≤ 1014) — вес кратчайшего пути и сумма весов рёбер в минимальном остовном дереве найденного графа.
В следующих m строках выведите рёбра графа. В каждой строке выведите три целых числа u, v, w (1 ≤ u, v ≤ n, 1 ≤ w ≤ 109) обозначающие ребро между вершинами u и v и имеющее вес w.
4 4
7 7
1 2 3
2 3 2
3 4 2
2 4 4
5 4
7 13
1 2 2
1 3 4
1 4 3
4 5 4
Граф из первого тестового примера: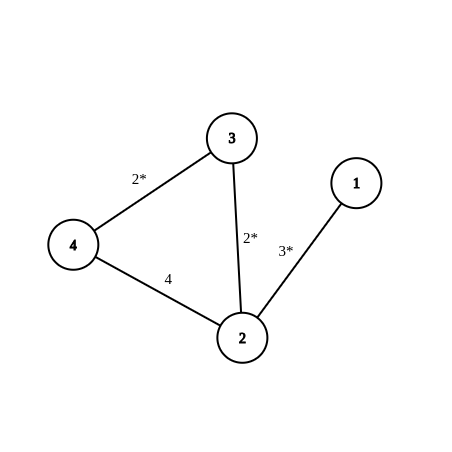 
Последовательность вершин в кратчайшем пути: {1, 2, 3, 4}. Рёбра минимального остовного дерева обозначены звёздочкой (*).
Определения терминов из условия:
Кратчайший путь в неориентированном графе — это последовательность вершин (v1, v2, ... , vk) такая, что существует ребро между vi и vi + 1 1 ≤ i < k и сумма весов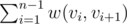 
минимальна, где w(i, j) — это вес ребра между вершинами i и j. (https://ru.wikipedia.org/wiki/Задача_о_кратчайшем_пути)
Простое число — это целое число, большее 1, такое, что у него нет положительных делителей отличных от 1 и этого числа. (https://ru.wikipedia.org/wiki/Простое_число)
Минимальное остовное дерево графа — это подмножество рёбер связного, неориентированного, взвешенного графа, соединяющее все вершины, не имеющее циклов и имеющее минимальную возможную сумму весов рёбер, в него входящих. (https://ru.wikipedia.org/wiki/Минимальное_остовное_дерево)
